海南省定安县2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-04-12 类型:期末考试
一、单选题
-
1. 二次根式 有意义,则 的取值范围是( )A、x>5 B、x<5 C、x≤5 D、x≥52. 下列二次根式中是最简二次根式的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、2 - =1 B、 + = C、 × =4 D、 ÷ =24. 方程 的左边配成完全平方后所得方程为( )A、 B、 C、 D、5. 方程:x(x+1)=3(x+1)的解的情况是( )A、x=﹣1 B、x=3 C、x1=﹣1,x2=3 D、以上答案都不对6. 已知锐角A,且sinA= ,则∠A等于( )A、60° B、45° C、30° D、15°7. 某公司2016年缴税70万元,2018年缴税90万元,求该公司这两年缴税的年平均增长率. 若设该公司这两年缴税的年平均增长率为x,根据题意,可得方程( )A、70x2=90 B、70(1+x)2=90 C、70(1+x)=90 D、70+70(1+x)+70(1+x)2=908. 一元二次方程x2+x+2=0的根的情况是( )A、有两个不相等的正实数根 B、有两个不相等的负实数根 C、有两个相等的实数根 D、没有实数根9. 如图,在 中, 分别是 边上的中点,则 ( )
 A、1 B、 C、 D、10. 如图,P是∠α的边OA上一点,且点P的横坐标为3,sinα= ,则tanα=( )
A、1 B、 C、 D、10. 如图,P是∠α的边OA上一点,且点P的横坐标为3,sinα= ,则tanα=( )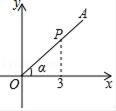 A、 B、 C、 D、11. 如图所示,若△ABC∽△DEF,则∠E的度数为( )
A、 B、 C、 D、11. 如图所示,若△ABC∽△DEF,则∠E的度数为( )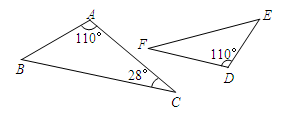 A、28° B、32° C、42° D、52°12. 在一个不透明的口袋中装有若干个质地相同而颜色可能不全相同的球,如果口袋中只装有3个黄球,且摸出黄球的概率为 ,那么袋中共有球 ( )A、6个 B、7个 C、9个 D、12个13. 从一副(54张)扑克牌中任意抽取一张,正好为K的概率为( )A、 B、 C、 D、14. 如图,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14m到达D,在D处测得A的仰角为45°,塔高AB为( )
A、28° B、32° C、42° D、52°12. 在一个不透明的口袋中装有若干个质地相同而颜色可能不全相同的球,如果口袋中只装有3个黄球,且摸出黄球的概率为 ,那么袋中共有球 ( )A、6个 B、7个 C、9个 D、12个13. 从一副(54张)扑克牌中任意抽取一张,正好为K的概率为( )A、 B、 C、 D、14. 如图,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14m到达D,在D处测得A的仰角为45°,塔高AB为( )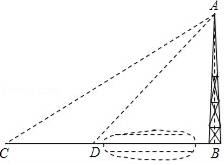 A、(16 -4) m B、(7 +7) m C、(16 +7) m D、(10 +7) m
A、(16 -4) m B、(7 +7) m C、(16 +7) m D、(10 +7) m二、填空题
-
15. 若 ,则 的值是 .16. 两个相似三角形的面积之比为4:25,则这两个三角形的周长比为.17. 某山坡坡面的坡度为1: ,则坡角是 度.
三、解答题
-
18.
学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为 .
 19. 计算:(1)、 - +(2)、2sin45°+8cos30°-tan60°(3)、2 cos45°- -3tan30°+20. 解方程:(1)、 ;(2)、 ;(3)、 .21. 如图,在一个 的正方形DEFG网格中有一个 .
19. 计算:(1)、 - +(2)、2sin45°+8cos30°-tan60°(3)、2 cos45°- -3tan30°+20. 解方程:(1)、 ;(2)、 ;(3)、 .21. 如图,在一个 的正方形DEFG网格中有一个 .
①在网格中画出 向下平移3个单位得到的 ;
②在网格中画出 绕C点逆时针方向旋转 得到的 ;
③若以 所在直线为x轴, 所在的直线为y轴建立直角坐标系,写出 , 两点的坐标.
22. 袋子中装有2个红球,1个黄球,它们除颜色外其余都相同。小明和小英做摸球游戏,约定一次游戏规则是:小英先从袋中任意摸出1个球记下颜色后放回,小明再从袋中摸出1个球记下颜色后放回,如果两人摸到的球的颜色相同,小英赢,否则小明赢.(1)、请用树状图或列表格法表示一次游戏中所有可能出现的结果;(2)、这个游戏规则对双方公平吗?请说明理由.

