贵州省贵阳市2019届九年级上学期数学期末考试试卷
试卷更新日期：2019-04-12 类型：期末考试
一、单选题
-
1. 观察下列每组图形，相似图形是（ ）A、
B、
C、
D、
2. 一元二次方程x2 +2x+4＝0的根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定3. 如图，AD∥BE∥CF，AB=3，BC=6，DE=2，则EF的值为（ ）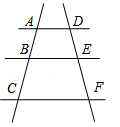
A、2 B、3 C、4 D、54. 如图，菱形ABCD的周长为28，对角线AC，BD交于点O，E为AD的中点，则OE的长等于（ ）
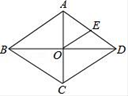A、2 B、3.5 C、7 D、145. 在一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其他完全相同，小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在15%和45%，则口袋中白色球的个数可能是（ ）A、24 B、18 C、16 D、66. 一个三角形三边的长分别为3,4,5,另一个与它相似的三角形的最长边是10,则其他两边的和是（ ）A、9 B、12 C、13 D、147. 祁中初三66班学生毕业时，每个同学都要给其他同学写一份毕业留言作为纪念，全班学生共写了930份留言．如果全班有x名学生，根据题意，列出方程为（ ）
A、 =930 B、 =930 C、x（x+1）=930 D、x（x﹣1）=9308. 已知点(x1 ,-1),(x2 , ),(x3 ,3)都在反比例函数 的图象上,则x1 ,x2,x3的大小关系是（ ）A、x1＞ x2＞x3 B、x1＞x3＞x2 C、x2＞x1 ＞x3 D、x3 ＞x1＞x29. 如图，矩形OABC的顶点O与平面直角坐标系的原点重合，点A，C分别在x轴，y轴上，点B的坐标为(－5，4)，点D为边BC上一点，连接OD，若线段OD绕点D顺时针旋转90°后，点O恰好落在AB边上的点E处，则点E的坐标为（ ）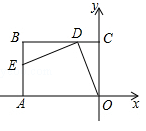
A、(－5，3） B、(－5，4) C、(－5， ） D、(－5，2)10. 将2019个边长为1的正方形按如图所示的方式排列，点A，A1 ， A2 ， A3 ， ……A2019和点M，M1 ， M2……，M2018是正方形的顶点，连接A1M，A2M1 ， A3M2 ， ……A2018分别交正方形的边A1M，A2M1 ， A3M2 ， ……A2018M2017于点N1 ， N2 ， N3……N2018 ， 四边形M1N1A1A2的面积是 ，四边形M2N2A2A3的面积是 ，…，则 为（ ）
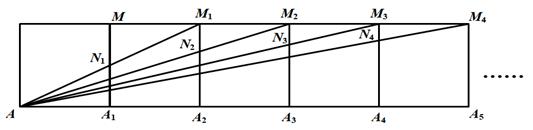A、 B、 C、 D、二、填空题
-
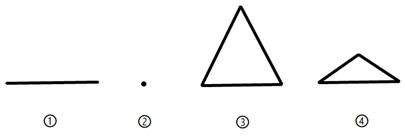
11. 小明拿一个等边三角形木板在阳光下玩，等边三角形木板在地面上形成的投影可能是.(填序号)
12. 已知正方形ABCD的对角线AC= ，则正方形ABCD的面积为 ．13. 若关于x的一元二次方程x2+mx+2n=0有一个根是2，则m+n= ．14. 如图，点A是反比例函数y＝ 的图象上的一点，过点A作AB⊥x轴，垂足为B，点C为y轴上的一点，连接AC、BC，若△ABC的面积为3，则k的值是 ．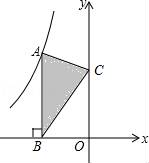
15. 在Rt△ABC中，∠BAC=90，AB=AC，AD⊥BC于点D，P是线段AD上的一个动点，以点P为直角的顶点，向上作等腰直角三角形PBE，连接DE，若在点P的运动过程中，DE的最小值为3，则AD的长为 ．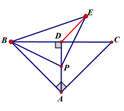
三、解答题
-
16. 画出如图所示立体图形的三视图.
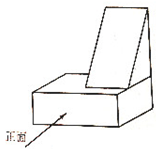17. 已知长方形硬纸板ABCD的长BC为40cm，宽CD为30cm，按如图所示剪掉2个小正方形和2个小长方形（即图中阴影部分），将剩余部分折成一个有盖的长方体盒子，设剪掉的小正方形边长为xcm．（纸板的厚度忽略不计）
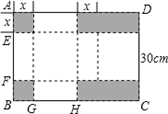(1)、填空：EF= ． cm，GH= ． cm；（用含x的代数式表示）(2)、若折成的长方体盒子的表面积为950cm2 ， 求该长方体盒子的体积18. 如图，在Rt△ABC中，∠ACB＝90°，AB＝6，过点C的直线MN∥AB，D为AB上一点，过点D作DE⊥BC，交直线MN于点E，垂足为F，连接CD，BE.
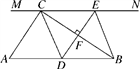(1)、当点D是AB的中点时，四边形BECD是什么特殊四边形？说明你的理由；(2)、在(1)的条件下，当∠A等于多少度时，四边形BECD是正方形？19. 如图，一块直角三角板的直角顶点P放在矩形ABCD的BC边上，并且使一条直角边经过点D，另一条直角边与AB交于点Q.
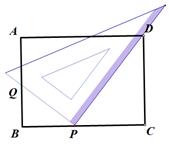(1)、请你写出一对相似三角形，并加以证明；(2)、若AB=6，BC=8，当PD=3PQ时，求PC的长.20. 如图，3×3的方格分为上中下三层，第一层有一枚黑色方块甲，可在方格A、B、C中移动，第二层有两枚固定不动的黑色方块，第三层有一枚黑色方块乙，可在方格D、E、F中移动，甲、乙移入方格后，四枚黑色方块构成各种拼图．
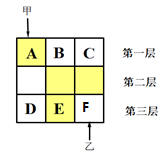(1)、若乙固定在E处，移动甲后黑色方块构成的拼图是轴对称图形的概率是多少；(2)、若甲、乙均可在本层移动，用画树状图法或列表法求出黑色方块所构成拼图是轴对称图形的概率．21. 在平面直角坐标系中，一次函数 的图象与 y轴交于点B(0，2)，与反比例函数 的图象交于点A (4，-1)．
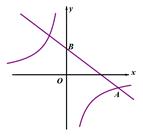(1)、求反比例函数的表达式和一次函数表达式；(2)、若点C是y轴上一点，且BC=BA，请直接写出点C的坐标．22. 如图，已知A，B两点的坐标分别为(40，0)和(0，30)，动点P从点A开始在线段AO上以每秒2个单位长度的速度向原点O运动，同时直线EF由x轴为起始位置以每秒1个单位长度的速度向上平行移动(即EF∥x轴)，并且分别与y轴、线段AB交于点E，F，连接EP，FP，设动点P与直线EF同时出发，运动时间为t秒．
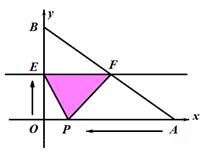(1)、求t=15秒时，求EF的长度；(2)、直线EF、点P在运动过程中，是否存在这样的t，使得△PEF的面积等于160(平方单位)?若存在，请求出此时的值；若不存在，请说明理由．