甘肃省白银市靖远县2019届九年级上学期数学期末考试试卷
试卷更新日期:2019-04-12 类型:期末考试
一、单选题
-
1.
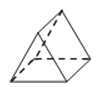
如图所示的几何体的左视图是( )
 A、
A、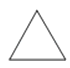 B、
B、 C、
C、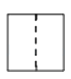 D、
D、 2.
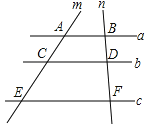
2.如图,已知直线a∥b∥c , 直线m、n与直线a、b、c分别交于点A、C、E、B、D、F , AC=4,CE=6,BD=3,则BF=( ).
 A、7 B、7.5 C、8 D、8.53. 在反比例函数y= 的图象的每一支位上,y随x的增大而减小,则m的取值范围是( )A、m>7 B、m<7 C、m=7 D、m≠74. 在一个不透明的袋子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中红球的个数约为( )A、4 B、6 C、8 D、125. 李明去参加聚会,每两人都互相赠送礼物,他发现共送礼物20件,若设有n人参加聚会,根据题意可列出方程为( )A、 =20 B、n(n﹣1)=20 C、 =20 D、n(n+1)=206. 两道单选题都含有A、B、C、D四个选项,瞎猜这两道题恰好全部猜对的概率是( )A、 B、 C、 D、7. 在四边形 中, 是对角线 、 的交点,能判定这个四边形为正方形的是( )A、 , B、 , , C、 , , D、 ,8. 如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若S△BDE∶S△CDE=1∶3,则S△DOE∶S△AOC的值为( )
A、7 B、7.5 C、8 D、8.53. 在反比例函数y= 的图象的每一支位上,y随x的增大而减小,则m的取值范围是( )A、m>7 B、m<7 C、m=7 D、m≠74. 在一个不透明的袋子中有20个除颜色外均相同的小球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后,发现摸到红球的频率稳定于0.4,由此可估计袋中红球的个数约为( )A、4 B、6 C、8 D、125. 李明去参加聚会,每两人都互相赠送礼物,他发现共送礼物20件,若设有n人参加聚会,根据题意可列出方程为( )A、 =20 B、n(n﹣1)=20 C、 =20 D、n(n+1)=206. 两道单选题都含有A、B、C、D四个选项,瞎猜这两道题恰好全部猜对的概率是( )A、 B、 C、 D、7. 在四边形 中, 是对角线 、 的交点,能判定这个四边形为正方形的是( )A、 , B、 , , C、 , , D、 ,8. 如图,D,E分别是△ABC的边AB,BC上的点,DE∥AC,若S△BDE∶S△CDE=1∶3,则S△DOE∶S△AOC的值为( )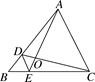 A、 B、 C、 D、9. 棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的表面积为( )
A、 B、 C、 D、9. 棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的表面积为( ) A、36cm2 B、33cm2 C、30cm2 D、27cm210. 如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数y=的图象经过点C,且与AB交于点E.若OD=2,则△OCE的面积为( )
A、36cm2 B、33cm2 C、30cm2 D、27cm210. 如图,已知四边形OABC是菱形,CD⊥x轴,垂足为D,函数y=的图象经过点C,且与AB交于点E.若OD=2,则△OCE的面积为( )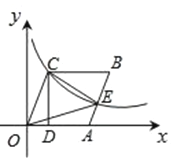 A、2 B、4 C、2 D、4
A、2 B、4 C、2 D、4二、填空题
-
11.
下面四幅图是两个物体不同时刻在太阳光下的影子,按照时间的先后顺序是 .
 12. 如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是.
12. 如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是. 13. 从长为10cm、7cm、5cm、3cm的四条线段中任选三条能够组成三角形的概率是 .14. 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少m处.(结果精确到0.1m)
13. 从长为10cm、7cm、5cm、3cm的四条线段中任选三条能够组成三角形的概率是 .14. 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少m处.(结果精确到0.1m) 15. 若关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是.16. 如图所示,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为.
15. 若关于 的一元二次方程 有两个不相等的实数根,则 的取值范围是.16. 如图所示,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为.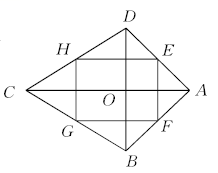 17. 一个几何体的三种视图如图所示,这个几何体的表面积是 . (结果保留π)
17. 一个几何体的三种视图如图所示,这个几何体的表面积是 . (结果保留π)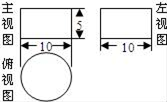 18. 已知函数y=y1+y2 , y1与x成正比例,y2与x成反比例,且当x=1时,y=4;当x=2时,y=5. y与x之间的函数关系式 , 当x=4时,求y= .
18. 已知函数y=y1+y2 , y1与x成正比例,y2与x成反比例,且当x=1时,y=4;当x=2时,y=5. y与x之间的函数关系式 , 当x=4时,求y= .三、解答题
-
19. 用适当方法解下列方程:(1)、x2+4x﹣1=0(2)、3x2﹣2=4x20. 如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
 (1)、请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.21. 如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).
(1)、请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.(2)、如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.21. 如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).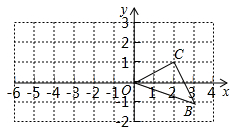 (1)、以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;(2)、分别写出B、C两点的对应点B′、C′的坐标;(3)、如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.22. 已知:如图,在矩形ABCD中,E为AD上一点,EF⊥CE,交AB于点F,DE=2,矩形的周长为16,且CE=EF.求AE的长.
(1)、以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;(2)、分别写出B、C两点的对应点B′、C′的坐标;(3)、如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.22. 已知:如图,在矩形ABCD中,E为AD上一点,EF⊥CE,交AB于点F,DE=2,矩形的周长为16,且CE=EF.求AE的长.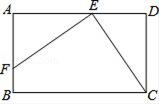 23. 如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.
23. 如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.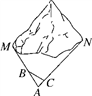 24. 长城公司为希望小学捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.(1)、写出所有的选购方案(用列表法或树状图);(2)、如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少?25. 商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价1元,商场平均每天可多售出2件.(1)、若某天该商品每件降价3元,当天可获利多少元?(2)、设每件商品降价x元,则商场日销售量增加件,每件商品,盈利元(用含x的代数式表示);(3)、在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到2000元?26. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
24. 长城公司为希望小学捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.(1)、写出所有的选购方案(用列表法或树状图);(2)、如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少?25. 商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价1元,商场平均每天可多售出2件.(1)、若某天该商品每件降价3元,当天可获利多少元?(2)、设每件商品降价x元,则商场日销售量增加件,每件商品,盈利元(用含x的代数式表示);(3)、在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到2000元?26. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.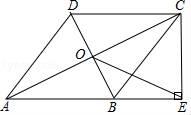 (1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.
(1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.