浙江省余姚市2018-2019学年七年级下学期数学3月月考试卷
试卷更新日期:2019-04-12 类型:月考试卷
一、单选题
-
1. 将如图所示的图案通过平移后可以得到的图案是( )
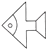 A、
A、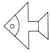 B、
B、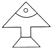 C、
C、 D、
D、 2. 下列是二元一次方程的是( )A、x+8y=0 B、2x2=y C、y+ =2 D、3x=103. 下列图形中,∠1与∠2是同位角的是( )A、
2. 下列是二元一次方程的是( )A、x+8y=0 B、2x2=y C、y+ =2 D、3x=103. 下列图形中,∠1与∠2是同位角的是( )A、 B、
B、 C、
C、 D、
D、 4. 以 为解的二元一次方程是( )A、2x-3y=-13 B、y=2x+5 C、y-4x=5 D、x=y-35. 如图所示,已知直线a∥b,c与a,b均相交,∠1=60°则∠2为( )
4. 以 为解的二元一次方程是( )A、2x-3y=-13 B、y=2x+5 C、y-4x=5 D、x=y-35. 如图所示,已知直线a∥b,c与a,b均相交,∠1=60°则∠2为( ) A、60° B、70° C、120° D、150°6. 如图所示,若∠A=75°,则要使EB∥AC可添加的条件是( )
A、60° B、70° C、120° D、150°6. 如图所示,若∠A=75°,则要使EB∥AC可添加的条件是( ) A、∠C=75° B、∠ABE=75° C、∠DBE=75° D、∠EBC=105°7. 下列计算不正确的是( )A、 B、 C、 D、8. 如图,三角形ABC沿着由点B到点E的方向平移到三角形DEF的位置,已知BC=8,EC=5,那么平移的距离为( )
A、∠C=75° B、∠ABE=75° C、∠DBE=75° D、∠EBC=105°7. 下列计算不正确的是( )A、 B、 C、 D、8. 如图,三角形ABC沿着由点B到点E的方向平移到三角形DEF的位置,已知BC=8,EC=5,那么平移的距离为( )
 A、13 B、8 C、5 D、39. 已知a、b满足方程组 ,则3a+b的值为( )A、-4 B、4 C、8 D、-810. 若P,Q是直线AB外不重合的两点,则下列说法不正确的是( )A、直线PQ可能与直线AB垂直 B、直线PQ可能与直线AB平行 C、过点P的直线一定能与直线AB相交 D、过点Q只能画出一条直线与AB平行11. 在迎宾晚宴上,若每桌坐12人,则空出3张桌子;若每桌坐10人,则还有12人不能就坐. 设有嘉宾x名,共准备了y张桌子. 根据题意,下列方程组正确的是( )A、 B、 C、 D、12. 用S(n)表示自然数n的各位数字之和,如S(1)=1,S(12)=3,S(516)=12,…,试问当n+S(n)=2015时,自然数n的值为( )A、1991 B、1993或2011 C、2011 D、1991或2013
A、13 B、8 C、5 D、39. 已知a、b满足方程组 ,则3a+b的值为( )A、-4 B、4 C、8 D、-810. 若P,Q是直线AB外不重合的两点,则下列说法不正确的是( )A、直线PQ可能与直线AB垂直 B、直线PQ可能与直线AB平行 C、过点P的直线一定能与直线AB相交 D、过点Q只能画出一条直线与AB平行11. 在迎宾晚宴上,若每桌坐12人,则空出3张桌子;若每桌坐10人,则还有12人不能就坐. 设有嘉宾x名,共准备了y张桌子. 根据题意,下列方程组正确的是( )A、 B、 C、 D、12. 用S(n)表示自然数n的各位数字之和,如S(1)=1,S(12)=3,S(516)=12,…,试问当n+S(n)=2015时,自然数n的值为( )A、1991 B、1993或2011 C、2011 D、1991或2013二、填空题
-
13. 计算 的结果是 .14. 请写出方程2x-y=3的一个解 .15. 如图,直线a∥b,直线c与直线a、b相交,若∠1=47º,则∠2的度数为 .
 16. 若方程 是二元一次方程,则a的值为.17. 如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论中①∠C′EF=32°;②∠AEC=116°;③∠BGE=64°;④∠BFD=116°,正确的有 .
16. 若方程 是二元一次方程,则a的值为.17. 如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论中①∠C′EF=32°;②∠AEC=116°;③∠BGE=64°;④∠BFD=116°,正确的有 . 18. 已知关于x,y的二元一次方程 ,若无论m取任何实数,该二元一次方程都有一个相同的解,则这个相同的解为 .
18. 已知关于x,y的二元一次方程 ,若无论m取任何实数,该二元一次方程都有一个相同的解,则这个相同的解为 .三、解答题
-
19. 计算下列各式,并用幂的形式表示结果.(1)、(2)、(3)、20. 解方程组(1)、(2)、21. 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
 (1)、请画出平移后的△A′B′C′;(2)、若连接AA′,CC′,则这两条线段之间的关系是、 .22. 已知方程组 的解x,y的和等于2,
(1)、请画出平移后的△A′B′C′;(2)、若连接AA′,CC′,则这两条线段之间的关系是、 .22. 已知方程组 的解x,y的和等于2,①求m的值.
②原方程组的解.
23. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.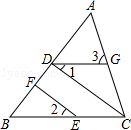 (1)、CD与EF平行吗?请说明理由.(2)、如果∠1=∠2,且∠3=60°,求∠ACB的度数.24. 下表为某主题公园的几种门票价格,李三同学用1600元作为购买门票的资金.
(1)、CD与EF平行吗?请说明理由.(2)、如果∠1=∠2,且∠3=60°,求∠ACB的度数.24. 下表为某主题公园的几种门票价格,李三同学用1600元作为购买门票的资金.门票种类
指定日普通票
平日普通票
夜票
票价(元/张)
200
160
100
(1)、李三若用全部资金购买“指定日普通票”和“夜票”共10张,则“指定日普通票”和“夜票”各买多少张?(2)、李三若想用全部资金购买“指定日普通票”“平日普通票”和“夜票”共10张(每种至少一张),请你帮他设计应如何购买?25. 如图1,已知直线CD∥EF,点A、B分别在直线CD与EF上.P为两平行线间一点.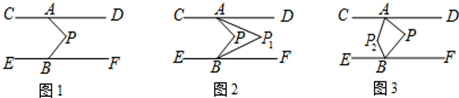 (1)、若∠DAP=40°,∠FBP=70°,则∠APB= .(2)、猜想∠DAP,∠FBP,∠APB之间有什么关系?并说明理由.(3)、利用(2)的结论解答:
(1)、若∠DAP=40°,∠FBP=70°,则∠APB= .(2)、猜想∠DAP,∠FBP,∠APB之间有什么关系?并说明理由.(3)、利用(2)的结论解答:①如图2,AP1、BP1分别平分∠DAP、∠FBP,请你写出∠P与∠P1的数量关系,并说明理由.
②如图3,AP2、BP2分别平分∠CAP、∠EBP,若∠APB=β,求∠AP2B(用含β的代数式表示).