湖北省武汉市青山区三校联考2018-2019学年七年级下学期数学3月月考试卷
试卷更新日期：2019-04-12 类型：月考试卷
一、单选题
-
1. 下列图形中∠1和∠2是对顶角的是（ ）A、
B、
C、
D、
2. 体育课上，老师测量小明跳远成绩的依据是（ ）A、过直线上一点且垂直于这条直线的直线有且只有一条 B、两点之间，线段最短 C、垂线段最短 D、两点确定一条直线3. 实数－π，－3.14，0， 四个数中，最小的是（ ）A、－π B、－3.14 C、 D、04. 如图，数轴上A、B两点表示的数分别为 和5.1，则A、B两点之间表示整数的点共有（ ）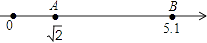
A、6个 B、5个 C、4个 D、3个5. 如图，AB∥CD，直线EF分别交AB，CD于E，F两点，∠BEF的平分线交CD于点G，若∠EFG=72°，则∠EGF等于（ ）
A、36° B、54° C、72° D、108°6. 如图所示，已知AC⊥BC，CD⊥AB，垂足分别是C，D，那么以下线段大小的比较必定成立的是（ ）
A、CD>AD B、AC<BC C、BC>BD D、CD<BD7. 如果 ，那么m的取值范围是（ ）A、0＜m＜1 B、1＜m＜2 C、2＜m＜3 D、3＜m＜48. 已知 ， ， ，则 的值是（ ）A、24.72 B、53.25 C、11.47 D、114.79. 把图中的一个三角形先横向平移x格，再纵向平移y格，就能与另一个三角形拼合成一个四边形，那么x+y（ ）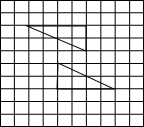
A、是一个确定的值 B、有两个不同的值 C、有三个不同的值 D、有三个以上不同的值10. 小明从A地向南偏东m°（0＜m＜90）的方向行走到B地，然后向左转30°行走到C地，则下面表述中，正确的个数是（ ）①B可能在C的北偏西m°方向；②当m＜60时，B在C的北偏西(m＋30)°方向；③B不可能在C的南偏西m°方向；④当m＞60时，B在C的南偏西(150－m)°方向
A、1 B、2 C、3 D、4二、填空题
-
11. 图是对顶角量角器，用它测量角度的原理是 ．
12. 比较大小： （填“＞”或“＜”）13. 已知2a－4和3a－1是同一个正数的两个平方根，则a＝ ， 这个正数是 ．14. 如图，将△ABC沿BC方向平移2cm 得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为 ．
15. 如图，AB∥CD，∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H，∠K－∠H＝33°，则∠K＝ ．
三、解答题
-
16. 计算：(1)、(2)、17. 求下列各式中的x．(1)、4x2=81；(2)、（x+1）3﹣27=0．18. 给下列证明过程填写理由．
如图，CD⊥AB于D，点F是BC上任意一点，EF⊥AB于E，∠1=∠2，求证：∠ACB=∠3．
请阅读下面解答过程，并补全所有内容．
解：∵CD⊥AB，EF⊥AB（已知）
∴∠BEF=∠BDC=90°（ ）
∴EF∥DC（ ）
∴∠2=__（ ）
又∵∠2=∠1（已知）
∴∠1=__（等量代换）
∴DG∥BC（ ）
∴∠3=__（ ）
19. 如图，每个小正方形的边长为1，在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′，利用网格点画图和无刻度的直尺画图并解答（保留画图痕迹）：
(1)、①画出△A′B′C′；②画出△ABC的高，即线段BD；
(2)、连接AA′、 CC′，那么AA′与CC′的关系是；线段AC扫过图形的面积为 ．20. 如图，已知∠EFG＋∠BDG=180°，∠DEF=∠B，求证：∠AED=∠C．
21. 图1中的长方形长为宽的3倍，将四个这样的长方形拼成图2中的大正方形．
(1)、若中间小正方形的面积是 ，问图1中的长方形的面积是多少 ？(2)、若大正方形的面积就比小正方形的面积大 ，求中间小正方形的面积.22. 点D在∠ABC内，点E为边BC上一点，连接DE、CD．
(1)、如图1，连接AE，若∠AED=∠A+∠D，求证：AB//CD．(2)、在（1）的结论下，过点A的直线MA//ED．①如图2，当点E在线段BC上时，猜想并验证∠MAB与∠CDE的数量关系；
②如图3，当点E在线段BC的延长线上时，猜想并验证∠MAB与∠CDE的数量关系．
23. 如图：五边形ABCDE中，AB∥CD，BC⊥AB，AB=BC=8，CD=5．
(1)、说明∠A，∠E，∠D之间的数量关系；(2)、平移五边形ABCDE，使D点移动到C点，画出平移后的五边形A'B'C'CE'，并求出顺次连接A、A'、E'、C、D、E、A各点所围成的图形的面积；(3)、在∠BAE和∠E'CD的内部取一点F，使∠EAF= ∠EAB，∠FCE'= ∠DCE' ，求∠AFC与∠AED之间的数量关系．