浙江省宁波市象山县2019届九年级下学期数学3月月考试卷

试卷更新日期：2019-04-12 类型：月考试卷

进入出卷网下载

一、单选题

1. “367 人中有 2 人同月同日生”这一事件是（）

A、随机事件 B、必然事件 C、不可能事件 D、确定事件

查看试题解析
2. 如果n边形的内角和是它外角和的4倍，则n等于（）

A、7 B、8 C、10 D、9

查看试题解析
3. 在平面直角坐标系xOy中，若点P（4，3）在⊙O内，则⊙O的半径r的取值范围是（）

A、0＜r＜4 B、3＜r＜4 C、4＜r＜5 D、r＞5

查看试题解析
4. 如图，在△ABC中，点D，E分别为边AB，AC上的点，且DE∥BC．若AD＝5，BD＝10，AE＝3，则CE的长为（）

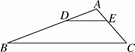A、3 B、6 C、9 D、12

查看试题解析
5. 如图，一根6m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A（羊只能在草地上活动）那么小羊A在草地上的最大活动区域面积是（）

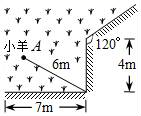A、9πm² B、 $\frac{29}{3}$ πm² C、15πm² D、 $\frac{31}{3}$ πm²

查看试题解析
6. 下列命题是真命题的是（）

A、直径是圆中最长的弦 B、三个点确定一个圆 C、平分弦的直径垂直于弦 D、相等的圆心角所对的弦相等

查看试题解析
7. 如图所示，在长为8cm，宽为6cm的矩形中，截去一个矩形（图中阴影部分），如果剩下的矩形与原矩形相似，那么剩下矩形的面积是（）

A、28cm² B、27cm² C、21cm² D、20cm²

查看试题解析
8. 已知（﹣1，y₁），（2，y₂），（3，y₃）在二次函数y＝﹣x²+4x+c的图象上，则y₁ ， y₂ ， y₃的大小关系正确的是（）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₃＜y₁＜y₂ D、y₁＜y₃＜y₂

查看试题解析
9. 如图，AB是⊙O的直径，点C，D在⊙O上，且点C，D在AB的异侧，连接AD，BD，OD，OC，若∠ABD＝15°，且AD∥OC，则∠BOC的度数为（）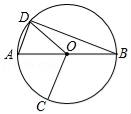

A、120° B、105° C、100° D、110°

查看试题解析
10. 已知二次函数y＝ax²+bx+c（a≠0）的图象如图，则下列结论错误的是（）

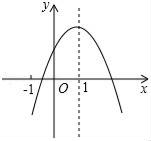A、4a+2b+c＞0 B、abc＜0 C、b＜a﹣c D、3b＞2c

查看试题解析
11. 如图，在Rt△ABC中，∠A＝90°，AB＝6，AC＝8，点D为边BC的中点，点M为边AB上的一动点，点N为边AC上的一动点，且∠MDN＝90°，则sin∠DMN为（）

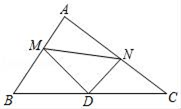A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{10}}{5}$

查看试题解析
12. 如图，在Rt△ABC中，BC＝3，∠BAC＝30°，斜边AB的两个端点分别在相互垂直的射线OM，ON上滑动．下列结论：①若C、O两点关于AB对称，则OA＝3 $\sqrt{3}$ ；②若AB平分CO，则AB⊥CO；③C，O两点间的最大距离是6；④斜边AB的中点D运动的路径长是 $\frac{3}{2}$ π，其中正确的有（）

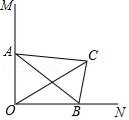A、①② B、③④ C、②③④ D、①③④

查看试题解析

二、填空题

13. 已知 $\frac{a}{b} = \frac{2}{3}$ ，则 $\frac{a}{a + b}$ 的值是．

查看试题解析
14. 在一个不透明的布袋中装有4个白球和n个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一个球，摸到白球的概率是 $\frac{1}{3}$ ，则n＝．

查看试题解析
15. 把抛物线y＝﹣（x﹣2）²﹣2先向左平移1个单位，再向下平移1个单位，得到的抛物线的解析式为。

查看试题解析
16. 如图，四边形ABCD是⊙O的内接四边形，AB是⊙O的直径，∠BCD＝130°，则∠ABD的度数是．

查看试题解析
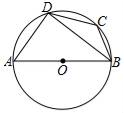17. 如图，将矩形ABCD绕点A按逆时针方向旋转一定角度后，BC的对应边B′C交CD边于点G，如果当AB′＝B′G时量得AD＝7，CG＝4，连接BB′、CC′，那么 $\frac{C C^{'}}{B B^{'}}$ ＝．

查看试题解析
18. 如图，⊙O过M点，⊙M交⊙O于A，延长⊙O的直径AB交⊙M于C，若AB＝8，BC＝1，则AM＝．

查看试题解析

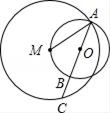
三、解答题

19. 计算：2cos30°﹣tan60°+sin30°+ $\frac{1}{2}$ tan45°．

查看试题解析

20. 王老师将

1

个黑球和若干个白球放入一个不透明的口袋并搅匀，让若干学生进行摸球实验，每次摸出一个球（有放回），下表是活动进行中的一组统计数据．

摸球的次数 $n$	$100$	$150$	$200$	$500$	$800$	$1000$
摸到黑球的次数 $m$	$23$	$31$	$60$	$130$	$203$	$249$
摸到黑球的频率 $\frac{m}{n}$	$0.23$	$0.21$	$0.30$	$0.26$	$0.253$

(1)、补全上表中的有关数据，根据上表数据估计从袋中摸出一个球是黑球的概率是（精确到0.01）；

(2)、估算袋中白球的个数；

(3)、在

(2)

的条件下，若小强同学有放回地连续两次摸球，用画树状图或列表的方法计算他两次都摸出白球的概率．

查看试题解析

21. 如图，两幢建筑物AB和CD，AB⊥BD，CD⊥BD，AB=15m，CD=20m．AB和CD之间有一景观池，小双在A点测得池中喷泉处E点的俯角为42°，在C点测得E点的俯角为45°，点B、E、D在同一直线上．求两幢建筑物之间的距离BD．（结果精确到0.1m）（参考数据：sin42°=0.67，cos42°=0.74，tan42°=0.90）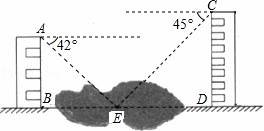

查看试题解析
22. 如图，一圆弧形钢梁

(1)、请用直尺和圆规补全钢梁所在圆

(2)、若钢梁的拱高为8米，跨径为40米，求这钢梁圆弧的半径。

查看试题解析
23. 如图，已知菱形ABCD，点E是AB的中点，AF⊥BC于点F，联结EF、ED、DF，DE交AF于点G，且AE²＝EG•ED．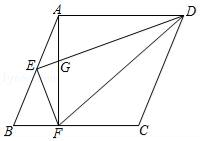

(1)、求证：DE⊥EF；

(2)、求证：BC²＝2DF•BF．

查看试题解析
24. 如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m．

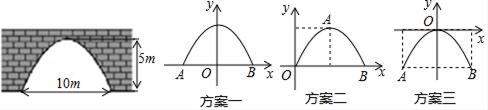(1)、经过讨论，同学们得出三种建立平面直角坐标系的方案（如图），你选择的方案是（填方案一，方案二，或方案三），则B点坐标是，求出你所选方案中的抛物线的表达式；

(2)、因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度．

查看试题解析
25. 如图所示，已知抛物线y＝﹣x²+bx+c与x轴相交于A、B两点，且点A的坐标为（1，0），与y轴交于点C，对称轴直线x＝2与x轴相交于点D，点P是抛物线对称轴上的一个动点，以每秒1个单位长度的速度从抛物线的顶点E向下运动，设点P运动的时间为t（s）．

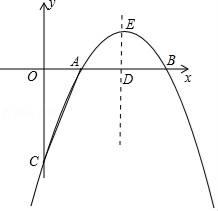(1)、点B的坐标为，抛物线的解析式是；

(2)、求当t为何值时，△PAC的周长最小？

(3)、当t为何值时，△PAC是以AC为腰的等腰三角形？

查看试题解析
26. 定义：若一个四边形能被其中的一条对角线分割成两个相似三角形，则称这个四边形为“友谊四边形”．我们熟知的平行四边形就是“友谊四边形”，

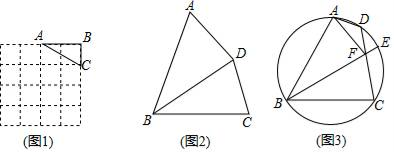(1)、如图1，在4×4的正方形网格中有一个Rt△ABC，请你在网格中找格点D，使得四边形ABCD是被AC分割成的“友谊四边形”，（要求画出点D的2种不同位置）

(2)、如图2，BD平分∠ABC，BD＝4 $\sqrt{3}$ ，BC＝8，四边形ABCD是被BD分割成的“友谊四边形”，求AB长；

(3)、如图3，圆内接四边形ABCD中，∠ABC＝60，点E是 $\overset{⏜}{A C}$ 的中点，连结BE交CD于点F，连结AF，∠DAF＝30°
①求证：四边形ABCF是“友谊四边形”；
②若△ABC的面积为6 $\sqrt{3}$ ，求线段BF的长．

查看试题解析