江苏省无锡市锡山区2019届九年级下学期数学3月月考试卷

试卷更新日期：2019-04-12 类型：月考试卷

进入出卷网下载

一、单选题

1. 方程x²＝2x的解是（）

A、2 B、0 C、0或2 D、都不是

查看试题解析
2. 如图，点A，B，C在⊙O上，∠ABO＝40°，∠ACO＝30°，则∠BOC的度数为（）

A、60° B、70° C、120° D、140°

查看试题解析
3. 甲、乙、丙、丁4对经过5轮选拔，平均分都相同，而方差依次为0.2、0.8、1.6、1.2．那么这4队中成绩最稳定的是（）

A、甲队 B、乙队 C、丙队 D、丁队

查看试题解析
4. 下列调查方式，你认为最合适的是（）

A、了解汕头市民春节期间出行方式，采用全面调查方式 B、游客上飞机前的安检，采用全面调查方式 C、了解汕头市每天的流动人口数，采用全面调查方式 D、日光灯管厂要检测一批灯管的使用寿命，采用全面调查方式

查看试题解析
5. 关于x的方程x²﹣2x﹣2＝0的根的情况是（）

A、有两个不等实根 B、有两个相等实根 C、没有实数根 D、无法判断根的情况

查看试题解析
6. 若一个圆锥的底面半径为3cm，母线长为5cm，则这个圆锥的全面积为（）

A、15π cm² B、24π cm² C、39π cm² D、48π cm²

查看试题解析
7. 如图，正五边形ABCDE内接于⊙O点F为 $\overset{⌢}{B C}$ 的中点，直线AP与⊙O相切于点A，则∠FAP的度数是（）

A、36° B、54° C、60° D、72°

查看试题解析
8. 如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线于点E，则下列结论错误的是（）

A、 $\frac{E D}{E A}$ ＝ $\frac{D F}{A B}$ B、 $\frac{D E}{C B}$ ＝ $\frac{E F}{F B}$ C、 $\frac{B F}{B E}$ ＝ $\frac{B C}{A E}$ D、 $\frac{B C}{D E}$ ＝ $\frac{B F}{B E}$

查看试题解析
9. 如图，已知等边△ABC的边长为8，以AB为直径的圆交BC于点F．以C为圆心，CF长为半径作图，D是⊙C上一动点，E为BD的中点，当AE最大时，BD的长为（）

A、 $4 \sqrt{3}$ B、 $4 \sqrt{5}$ C、 $4 \sqrt{3} + 2$ D、12

查看试题解析
10. 二次函数y＝ax²+bx+c的图象如图所示，以下结论：①abc＞0；②4ac＜b²；③2a+b＞0；④其顶点坐标为（ $\frac{1}{2}$ ，﹣2）；⑤当x＜ $\frac{1}{2}$ 时，y随x的增大而减小；⑥a+b+c＞0；⑦方程ax²+bx+c＝﹣4有实数解，正确的有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

11. 抛物线 y＝3（x+2）²﹣7 的对称轴是．

查看试题解析
12. 已知y₁=(x+3)²,y₂=2x+5.当x=时，y₁=y₂.

查看试题解析
13. 若x²+2x＝1，则2x²+4x+3的值是．

查看试题解析
14. 若一人患了流感，经过两轮传染后共有121人感染了流感．按照这样的传染速度，若2人患了流感，第一轮传染后患流感的人数共有人．

查看试题解析
15. 如图，在△ABC中，D为AB边上一点，△CBD∽△ACD，AD=6，BD=9，那么AC的长等于．

查看试题解析
16. 菱形 $A B C D$ 的边长为 $5$ ，面积为 $20$ ，则 $∠ A C B$ 的正切值为．

查看试题解析
17. 在四边形ABCD中，∠C=90°，DC=3，BC=4，AD=12，AB=13，则四边形ABCD的面积是．

查看试题解析

三、解答题

18. 如图，某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°，沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°．已知BC＝90米，且B、C、D在同一条直线上，山坡坡度i＝5：12．

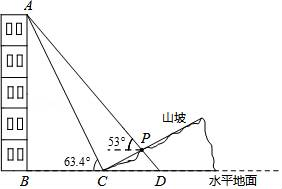(1)、求此人所在位置点P的铅直高度．(结果精确到0.1米)

(2)、求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)(测倾器的高度忽略不计，参考数据：tan53°≈ $\frac{4}{3}$ ，tan63.4°≈2)

查看试题解析
19. （ $\frac{1}{2}$ ）²﹣（2018﹣2019）⁰+（ $\sqrt{2}$ +1）（ $\sqrt{2}$ ﹣1）+ $\sqrt{3}$ tan30°

查看试题解析
20. 解下列方程或不等式组：

(1)、2x²﹣7x+3＝0；

(2)、 ${\begin{matrix} 1 - 3 (x - 1) < 8 - x \\ \frac{x - 3}{2} + 3 \geq x + 1 \end{matrix}$ ．

查看试题解析
21. 已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

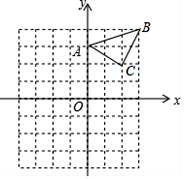(1)、△ABC向下平移4个单位长度得到的△A₁B₁C₁ ，点C₁的坐标是；

(2)、以点B为位似中心，在网格内画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是；（画出图形）

(3)、△A₂B₂C₂的面积是平方单位．

查看试题解析
22. 有4张卡片，正面分别写上1，2，3，4，它们的背面都相同．现将它们背面朝上，先从中任意摸出一张，卡片不放回，再任意摸出一张．

(1)、请用树状图或列表法表示出所有可能的结果．

(2)、求摸出的两张卡片上的数之和大于5的概率．

查看试题解析
23. 如图，已知⊙O是△ABC的外接圆，连接OC，过点A作AD∥OC，交BC的延长线于D，AB交OC于E，∠ABC＝45°．

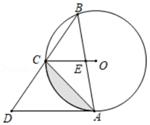(1)、求证：AD是⊙O的切线；

(2)、若AE＝ $\sqrt{17}$ ，CE＝3．
①求⊙O的半径；

②求图中阴影部分的面积．

查看试题解析
24. 如图，在A岛附近，半径约为250km的范围内是暗礁区，往北300km处有一灯塔B，往西400千米处有一灯塔C，现有一渔船沿CB航行，渔船是否会进入暗礁区？说明理由．

查看试题解析
25. 感知：如图①，在四边形ABCD中，AB∥CD，∠B=90°，点P在BC边上，当∠APD=90°时，可知△ABP∽△PCD．（不要求证明）
探究：如图②，在四边形ABCD中，点P在BC边上，当∠B=∠C=∠APD时，求证：△ABP∽△PCD．

拓展：如图③，在△ABC中，点P是边BC的中点，点D、E分别在边AB、AC上．若∠B=∠C=∠DPE=45°，BC=6 $\sqrt{2}$ ，CE=4，求DE的长

查看试题解析
26. 如图在平面直角坐标系xOy中，O为坐标原点，二次函数y=x²+bx+c的图象经过点A（3，0）、点B（0，3），顶点为M．

(1)、求该二次函数的解析式；

(2)、求∠OBM的正切值．

查看试题解析
27. 问题发现．

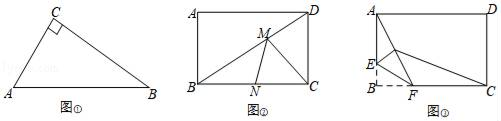(1)、如图①，Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点D是AB边上任意一点，则CD的最小值为．

(2)、如图②，矩形ABCD中，AB＝3，BC＝4，点M、点N分别在BD、BC上，求CM+MN的最小值．

(3)、如图③，矩形ABCD中，AB＝3，BC＝4，点E是AB边上一点，且AE＝2，点F是BC边上的任意一点，把△BEF沿EF翻折，点B的对应点为G，连接AG、CG，四边形AGCD的面积是否存在最小值，若存在，求这个最小值及此时BF的长度．若不存在，请说明理由．

查看试题解析