浙江省温州市2019届数学中考模拟试卷

试卷更新日期：2019-04-12 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的绝对值是（）

A、3 B、-3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 下列几何体中，其主视图为三角形的是（）

A、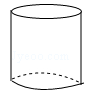 B、 C、 D、

查看试题解析
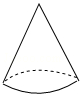3. 如图，已知AB∥DE，∠ABC＝75°，∠CDE＝145°，则∠BCD的值为（）

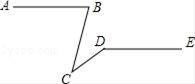A、20° B、30° C、40° D、70°

查看试题解析
4. 不等式x≤﹣1的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
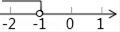5. 据调查，某班30位同学所穿鞋子的尺码如下表所示：则该班这30位同学所穿鞋子尺码的众数是（）

码号/码

33

34

35

36

37

人数

3

6

8

8

5

A、8 B、35 C、36 D、35和36

查看试题解析
6. 下列解方程去分母正确的是（）

A、由 $\frac{x}{3} - 1 = \frac{1 - x}{2}$ ，得2x﹣1＝3﹣3x B、由 $\frac{x - 2}{2} - \frac{x}{4} = - 1$ ，得2x﹣2﹣x＝﹣4 C、由 $\frac{y}{3} - 1 = \frac{y}{5}$ ，得2y-15=3y D、由 $\frac{y + 1}{2} = \frac{y}{3} + 1$ ，得3(y+1)＝2y+6

查看试题解析
7. 在Rt△ABC中，∠C＝90°，∠A＝15°，AB的垂直平分线与AC交于点M，则BC与MB的比为（）

A、1：3 B、1：2 C、2：3 D、3：4

查看试题解析
8. “凤鸣”文学社在学校举行的图书共享仪式上互赠图书，每个同学都把自己的图书向本组其他成员赠送一本，某组共互赠了210本图书，如果设该组共有x名同学，那么依题意，可列出的方程是 $($ $)$

A、 $x (x + 1) = 210$ B、 $x (x - 1) = 210$ C、 $2 x (x - 1) = 210$ D、 $\frac{1}{2} x (x - 1) = 210$

查看试题解析
9. 如图，以G（0，1）为圆心，半径为2的圆与x轴交于A，B两点，与y轴交于C，D两点，点E为⊙G上一动点，CF⊥AE于F．当点E从点B出发顺时针运动到点D时，点F所经过的路径长为（）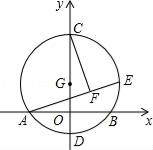

A、 $\frac{\sqrt{3}}{2} π$ B、 $\frac{\sqrt{3}}{3} π$ C、 $\frac{\sqrt{3}}{4} π$ D、 $\frac{\sqrt{3}}{6} π$

查看试题解析
10. 如图，在平面直角坐标系中，点P(1，4)、Q(m，n)在函数y＝ $\frac{k}{x}$ (k＞0)的图象上，当m＞1时，过点P分别作x轴、y轴的垂线，垂足为点A，B；过点Q分别作x轴、y轴的垂线，垂足为点C，D，QD交PA于点E，随着m的增大，四边形ACQE的面积（）

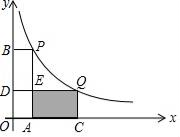A、增大 B、减小 C、先减小后增大 D、先增大后减小

查看试题解析

二、填空题

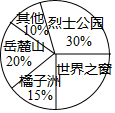
11. 因式分解：1﹣4a²＝．

查看试题解析
12. 如果一组数据 $1, 3, 5, a, 8$ 的方差是 $0.7$ ，则另一组数据 $11, 13, 15, a + 10, 18$ 的方差是．

查看试题解析
13. 若函数y=2x+b（b为常数）的图象经过点A（0，﹣2），则b= ．

查看试题解析
14. 某校九年级准备开展春季研学活动，对全年级学生各自最想去的活动地点进行了调查，把调查结果制成了如下扇形统计图，则“世界之窗”对应扇形的圆心角为度．

查看试题解析
15. 如图，在Rt△ABC中，∠B＝90°，AB＝2 $\sqrt{5}$ ，BC＝ $\sqrt{5}$ .将△ABC绕点A按逆时针方向旋转90°得到△AB′C′，连结B′C，则sin ∠ACB′＝．

查看试题解析
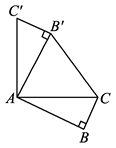16. 如图，已知AB是⊙O的直径，CD是⊙O的切线，C为切点，且∠BAC=50°，则∠ACD=°．

查看试题解析

三、解答题

17. 计算

(1)、(x＋y)²－2x(x＋y)；

(2)、(a＋1)(a－1)－(a－1)²；

(3)、先化简，再求值：
(x＋2y)(x－2y)－(2x³y－4x²y²)÷2xy，其中x=－3， $y = \frac{1}{2}$ .

查看试题解析
18. 如图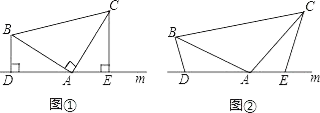

(1)、已知，如图①，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，求证：DE＝BD+CE．

(2)、如图②，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意钝角，请问结论DE＝BD+CE是否成立？若成立，请你给出证明：若不成立，请说明理由．

查看试题解析
19. 图①、图②都是4×4的正方形网格，每个小正方形的顶点为格点，每个小正方形的边长均为1．在图①、图②中已画出线段AB，点A、B均在格点上按下列要求画图：

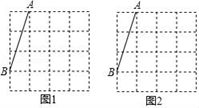(1)、在图①中，以格点为顶点，AB为腰，画一个三边长都是无理数的等腰三角形；

(2)、在图②中，以格点为顶点，AB为底的等腰三角形．

查看试题解析
20. 如图，⊙O的直径AB长为12，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．

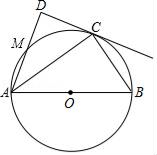(1)、求证：AC平分∠DAB．

(2)、设AD交⊙O于点M，当∠B＝60°时，求弧AM的长．

查看试题解析
21. 某工厂去年的利润（总收入﹣总支出）为300万元，今年总收入比去年增加20%，总支出比去年减少10%，今年的利润为420万元，去年的总收入、总支出各是多少万元？

查看试题解析
22. 如图，抛物线y=x²+bx+c与x轴交于点A和B（3，0），与y轴交于点C（0，3）．

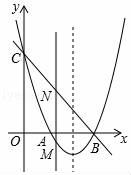(1)、求抛物线的解析式；

(2)、若点M是抛物线上在x轴下方的动点，过M作MN∥y轴交直线BC于点N，求线段MN的最大值；

(3)、E是抛物线对称轴上一点，F是抛物线上一点，是否存在以A，B，E，F为顶点的四边形是平行四边形？若存在，请直接写出点F的坐标；若不存在，请说明理由．

查看试题解析
23. 如图，在矩形ABCD中，AB＝3，BC＝4，将对角线AC绕对角线交点O旋转，分别交边AD、BC于点E、F，点P是边DC上的一个动点，且保持DP＝AE，连接PE、PF，设AE＝x（0＜x＜3）．

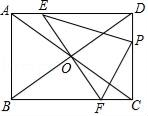(1)、填空：PC＝， FC＝（用含x的代数式表示）

(2)、求△PEF面积的最小值；

(3)、在运动过程中，PE⊥PF是否成立？若成立，求出x的值；若不成立，请说明理由．

查看试题解析

码号/码	33	34	35	36	37
人数	3	6	8	8	5