四川省成都市2019届九年级数学中考模拟试卷
试卷更新日期:2019-04-12 类型:中考模拟
一、单选题
-
1. 在实数0,﹣ , ,﹣2中,最小的是( )A、﹣2 B、﹣ C、0 D、2. 在函数y= 中,自变量x的取值范围是( )A、x> B、x≤ C、x≠ D、x≥3. 四川省是全国重要的蔬菜主产区、“南菜北运”和冬春蔬菜优势区,位于成都市彭州濛阳镇的四川省农产品交易中心,日交量超过5000吨,年交易额超过150亿元,是省内设施最先进,交易量最大的蔬菜专业批发市场,也是全国第二大蔬菜产地交易中心。已初步形成了“西部第一、全国一流”绿色蔬菜产业和“农工贸一体化、产加销一条龙”的发展新格局。其中150亿元,用科学记数法表示为( )A、1.5×102元 B、1.5×1011元 C、1.5×1010元 D、15×109元4. 一个几何体的三种视图如图所示,则这个几何体是( )
 A、长方体 B、圆锥 C、圆台 D、圆柱5. 若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是( )A、﹣5 B、﹣3 C、3 D、16. 如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,∠ADE=35°,∠C=120°,则∠A为( )
A、长方体 B、圆锥 C、圆台 D、圆柱5. 若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是( )A、﹣5 B、﹣3 C、3 D、16. 如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,∠ADE=35°,∠C=120°,则∠A为( )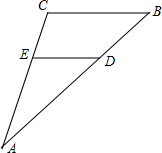 A、60° B、45° C、35° D、25°7. 分式方程 的解为( )A、x=1 B、x=2 C、无解 D、x=48. 如图,正方形ABCD内接于⊙O,AB=2 ,则 的长是( )
A、60° B、45° C、35° D、25°7. 分式方程 的解为( )A、x=1 B、x=2 C、无解 D、x=48. 如图,正方形ABCD内接于⊙O,AB=2 ,则 的长是( )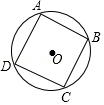 A、π B、 π C、2π D、 π9. 如图所示,▱ABCD中,EF过对角线的交点O,如果AB=6cm,AD=5cm,OF=2cm,那么四边形BCEF的周长为( )
A、π B、 π C、2π D、 π9. 如图所示,▱ABCD中,EF过对角线的交点O,如果AB=6cm,AD=5cm,OF=2cm,那么四边形BCEF的周长为( )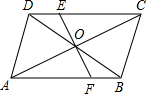 A、13cm B、15cm C、11cm D、9.5cm10. 如图,二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,则下列说法错误的是( )
A、13cm B、15cm C、11cm D、9.5cm10. 如图,二次函数y=x2﹣2x﹣3的图象与x轴交于A、B两点,与y轴交于点C,则下列说法错误的是( ) A、AB=4 B、∠ABC=45° C、当x>0时,y<﹣3 D、当x>1时,y随x的增大而增大
A、AB=4 B、∠ABC=45° C、当x>0时,y<﹣3 D、当x>1时,y随x的增大而增大二、解答题
-
11. 分解因式3x3﹣12x2y+12xy2=.12.(1)、计算:|﹣ |+ ﹣4sin45°﹣ .(2)、解不等式组 ,并把它的解集在如下的数轴上表示出来.13. 如图,我国海监船在钓鱼岛附近的O处观测到一可疑船正匀速直线航行我国海域,当该可疑船位于点O的北偏东30°方向上的点A处(OA=20 km)时,我方开始向对方喊话,但该可疑船仍匀速航行,40min后,又测得该可疑船位于点O的正北方向上的点B处,且OB=20km,求该可疑船航行的速度.
 14. 先化简,再求值: ,其中a= ﹣2.15. 如图是一间摄影展览厅,其东、西面各有一个入口A、B,南面为出口C,北面分别有两个出口D、E,摄影爱好者郑浩任选一个入口进入展览厅,参观结束后,任选一个出口离开。
14. 先化简,再求值: ,其中a= ﹣2.15. 如图是一间摄影展览厅,其东、西面各有一个入口A、B,南面为出口C,北面分别有两个出口D、E,摄影爱好者郑浩任选一个入口进入展览厅,参观结束后,任选一个出口离开。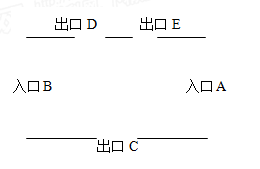 (1)、郑浩从进入到离开共有多少种可能的结果?请画出树形图;(2)、求出郑浩从入口A进入展览厅并从北面出口离开的概率。16. 如图,直线y=﹣x+2与反比例函数y= (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(1)、郑浩从进入到离开共有多少种可能的结果?请画出树形图;(2)、求出郑浩从入口A进入展览厅并从北面出口离开的概率。16. 如图,直线y=﹣x+2与反比例函数y= (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D. (1)、求a,b的值及反比例函数的解析式;(2)、若点P在直线y=﹣x+2上,且S△ACP=S△BDP , 请求出此时点P的坐标;(3)、在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.17. 如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C= ∠P.
(1)、求a,b的值及反比例函数的解析式;(2)、若点P在直线y=﹣x+2上,且S△ACP=S△BDP , 请求出此时点P的坐标;(3)、在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.17. 如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C= ∠P.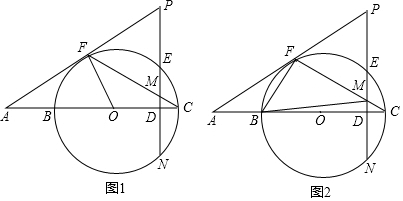 (1)、求证:PA是⊙O的切线;(2)、若∠A=30°,⊙O的半径为4,DM=1,求PM的长;(3)、如图2,在(2)的条件下,连结BF、BM;在线段DN上有一点H,并且以H、D、C为顶点的三角形与△BFM相似,求DH的长度.18. 在茶节期间,某茶商订购了甲种茶叶90吨,乙种茶叶80吨,准备用A、B两种型号的货车共20辆运往外地.已知A型货车每辆运费为0.4万元,B型货车每辆运费为0.6万元.(1)、设A型货车安排x辆,总运费为y万元,写出y与x的函数关系式;(2)、若一辆A型货车可装甲种茶叶6吨,乙种茶叶2吨;一辆B型货车可装甲种茶叶3吨,乙种茶叶7吨.按此要求安排A、B两种型号货车一次性运完这批茶叶,共有哪几种运输方案?(3)、说明哪种方案运费最少?最少运费是多少万元?19. 阅读下面材料:
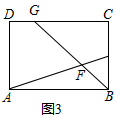
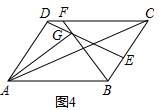
(1)、求证:PA是⊙O的切线;(2)、若∠A=30°,⊙O的半径为4,DM=1,求PM的长;(3)、如图2,在(2)的条件下,连结BF、BM;在线段DN上有一点H,并且以H、D、C为顶点的三角形与△BFM相似,求DH的长度.18. 在茶节期间,某茶商订购了甲种茶叶90吨,乙种茶叶80吨,准备用A、B两种型号的货车共20辆运往外地.已知A型货车每辆运费为0.4万元,B型货车每辆运费为0.6万元.(1)、设A型货车安排x辆,总运费为y万元,写出y与x的函数关系式;(2)、若一辆A型货车可装甲种茶叶6吨,乙种茶叶2吨;一辆B型货车可装甲种茶叶3吨,乙种茶叶7吨.按此要求安排A、B两种型号货车一次性运完这批茶叶,共有哪几种运输方案?(3)、说明哪种方案运费最少?最少运费是多少万元?19. 阅读下面材料:小明遇到这样一个问题:如图1,在正方形ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若AB=6,AF=4EF,求CG的值与∠AFB的度数.
他的做法是:过点E作EH∥AB交BG于点H,得到△BAF∽△HEF(如图2).


 (1)、CG等于多少,∠AFB等于多少度;
(1)、CG等于多少,∠AFB等于多少度;参考小明思考问题的方法,解决下列问题;
(2)、如图3,在矩形ABCD中,点E是边BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若AF=3EF,求 的值;(3)、如图4,在平行四边形ABCD中,E、F分别是边BC、CD上的点,BF和DE相交于点G,且AB=kAD,∠DAG=∠BAC,求出 的值(用含k的式子表示)20. 如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.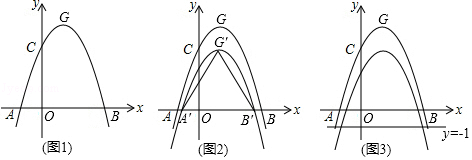 (1)、求出抛物线C1的解析式,并写出点G的坐标;(2)、如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2 , 设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:(3)、在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.
(1)、求出抛物线C1的解析式,并写出点G的坐标;(2)、如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2 , 设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:(3)、在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.三、填空题
-
21. 某课外小组调查了20户家庭某月的用电量,如下表所示
用电量(千瓦时)
120
140
160
180
200
户数
2
3
6
7
2
则这20户家庭该月用电量的平均数是(千瓦时),中位数是(千瓦时).
22. 已知反比例函数y= ,当x≥3时,则y的取值范围是 .23. 如图,在△ABC中,AB=5,AC=4,BC=3,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB、AC于点M、N;②分别以点M、N为圆心,以大于 的长为半径作弧,两弧相交于点E;③作射线AE;④以同样的方法作射线BF,AE交BF于点O,连接OC,则OC=.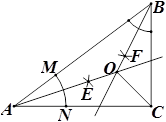 24. 已知a,b为一元二次方程x2+2x﹣9=0的两个根,那么a2+a﹣b的值为 .25. 在一个不透明的盒子里装有4个分别写有数字﹣2,﹣1,0,1,2的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将该小球上的数字为m,点P的坐标为(m,m2+1),则点P落在抛物线y=﹣4x2+8x+5与x轴所围成的区域内(含边界)的概率是 .26. 如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4 ,OD=2,点G在矩形内部,且∠GCB=30°,GC=2 ,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是 .
24. 已知a,b为一元二次方程x2+2x﹣9=0的两个根,那么a2+a﹣b的值为 .25. 在一个不透明的盒子里装有4个分别写有数字﹣2,﹣1,0,1,2的小球,它们除数字不同外其余全部相同,现从盒子里随机取出一个小球,将该小球上的数字为m,点P的坐标为(m,m2+1),则点P落在抛物线y=﹣4x2+8x+5与x轴所围成的区域内(含边界)的概率是 .26. 如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4 ,OD=2,点G在矩形内部,且∠GCB=30°,GC=2 ,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是 .

