陕西省2019届九年级数学中考一模试卷
试卷更新日期:2019-04-12 类型:中考模拟
一、单选题
-
1. 的相反数是A、 B、2019 C、- D、2. 一个几何体的三视图如图所示,则这个几何体是( )
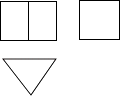 A、圆柱 B、圆锥 C、三棱柱 D、长方体3. 如图,直线l1∥l2 , 且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=52°,则∠2的度数为( )
A、圆柱 B、圆锥 C、三棱柱 D、长方体3. 如图,直线l1∥l2 , 且分别与直线l交于C,D两点,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=52°,则∠2的度数为( )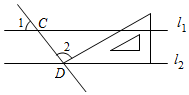 A、92° B、98° C、102° D、108°4. 点A(﹣3,2)在反比例函数y= (k≠0)的图象上,则k的值是( )
A、92° B、98° C、102° D、108°4. 点A(﹣3,2)在反比例函数y= (k≠0)的图象上,则k的值是( )
A、﹣6 B、﹣ C、﹣1 D、65. 下列运算正确的是A、2m2+m2=3m4 B、(mn2)2=mn4 C、2m·4m²=8m² D、m5÷m3=m26. 如图,四边形ABCD中∠DAB=60°,∠B=∠D=90°,BC=1,CD=2,则对角线AC的长为( )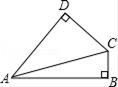 A、 B、 C、 D、7. 已知直线l: 与x轴交于点P,将l绕点P顺时针旋转90°得到直线 ,则直线 的解析式为A、 B、 C、 D、8. 如图,矩形ABCD中, , ,点E,F,G,H分别是矩形AB,BC,CD,DA的中点,则四边形EFGH的周长为
A、 B、 C、 D、7. 已知直线l: 与x轴交于点P,将l绕点P顺时针旋转90°得到直线 ,则直线 的解析式为A、 B、 C、 D、8. 如图,矩形ABCD中, , ,点E,F,G,H分别是矩形AB,BC,CD,DA的中点,则四边形EFGH的周长为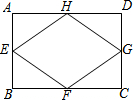 A、10 B、5 C、 D、9. 如图所示,点A,B,C,D在 上,CD是直径, ,则 的度数为
A、10 B、5 C、 D、9. 如图所示,点A,B,C,D在 上,CD是直径, ,则 的度数为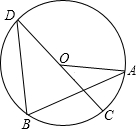 A、 B、 C、 D、10. 抛物线 的部分图象如图所示,与x轴的一个交点坐标为 ,抛物线的对称轴是 下列结论中: ; ; 方程 有两个不相等的实数根; 抛物线与x轴的另一个交点坐标为 ; 若点 在该抛物线上,则 .其中正确的有
A、 B、 C、 D、10. 抛物线 的部分图象如图所示,与x轴的一个交点坐标为 ,抛物线的对称轴是 下列结论中: ; ; 方程 有两个不相等的实数根; 抛物线与x轴的另一个交点坐标为 ; 若点 在该抛物线上,则 .其中正确的有 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
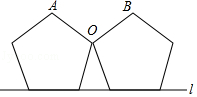
11. 比较大小: .12. 两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于度.
 13. 已知同一个反比例函数图象上的两点P1(x1 , y1)、P2(x2 , y2),若x2=x1+2,且 ,则这个反比例函数的解析式为 .14. 如图,在▱ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若 , ,则图中阴影部分的面积为 .
13. 已知同一个反比例函数图象上的两点P1(x1 , y1)、P2(x2 , y2),若x2=x1+2,且 ,则这个反比例函数的解析式为 .14. 如图,在▱ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若 , ,则图中阴影部分的面积为 .
三、解答题
-
15. 计算:16. 先化简,再求值: ,其中17. 某服装厂每天生产A、B两种品牌的服装共600件,A、B两种品牌的服装每件的成本和利润如表:设每天生产A种品牌服装x件,每天两种服装获利y元.
A
B
成本 元 件
50
35
利润 元 件
20
15
(1)、请写出y关于x的函数关系式;(2)、如果服装厂每天至少投入成本26400元,那么每天至少获利多少元?18. 如图,已知 中, ,请作 的外接圆 保面作图痕迹,不写作法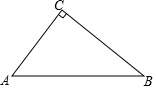 19. 如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.求证:AD与BE互相平分.
19. 如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O.求证:AD与BE互相平分. 20. 为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
20. 为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.学生立定跳远测试成绩的频数分布表
分组
频数
1.2≤x<1.6
a
1.6≤x<2.0
12
2.0≤x<2.4
b
2.4≤x<2.8
10
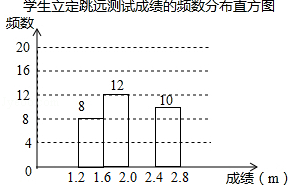
请根据图表中所提供的信息,完成下列问题:
(1)、表中a= , b= , 样本成绩的中位数落在范围内;(2)、请把频数分布直方图补充完整;(3)、该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?21. 城墙作为古城西安的地标性建筑,自然是吸引了不少人慕名而来,每逢春节,城墙上都会支起万盏花灯,小画和小明去城墙观赏花灯,看见宏伟的城墙后,他们想要测量城墙的高,小明在城墙下看见城墙上有一根灯杆 点A为灯泡的位置 ,于是小明提议用灯下的影长来测量城墙的高,首先小明站在E处,测得其影长 ,小画站在H处,测得其影长 ,小画和小明之间的距离 ,已知小明的身高DE为 ,小画的身高GH为 ,灯杆AB的高为 ,点B在直线AC上, , , 请你根据以上信息,求出城墙的高BC.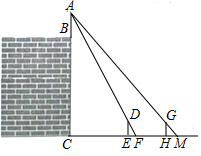 22. 某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
22. 某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)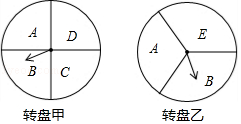 (1)、若顾客选择方式一,则享受9折优惠的概率为多少;(2)、若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.23. 如图,点 是 的边 上一点, 与边 相切于点 ,与边 , 分别相交于点 , ,且 .
(1)、若顾客选择方式一,则享受9折优惠的概率为多少;(2)、若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.23. 如图,点 是 的边 上一点, 与边 相切于点 ,与边 , 分别相交于点 , ,且 .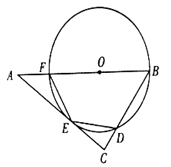 (1)、求证: ;(2)、当 , 时,求 的长.24. 如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.
(1)、求证: ;(2)、当 , 时,求 的长.24. 如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点,与y轴交于点C,其顶点为P,连接PA、AC、CP,过点C作y轴的垂线l.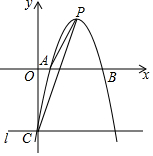 (1)、求点P,C的坐标;(2)、直线l上是否存在点Q,使 的面积等于 的面积的2倍?若存在,求出点Q的坐标;若不存在,请说明理由.25. 问题发现.
(1)、求点P,C的坐标;(2)、直线l上是否存在点Q,使 的面积等于 的面积的2倍?若存在,求出点Q的坐标;若不存在,请说明理由.25. 问题发现.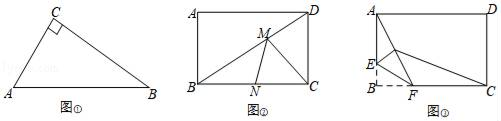 (1)、如图①,Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB边上任意一点,则CD的最小值为 .(2)、如图②,矩形ABCD中,AB=3,BC=4,点M、点N分别在BD、BC上,求CM+MN的最小值.(3)、如图③,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是BC边上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG、CG,四边形AGCD的面积是否存在最小值,若存在,求这个最小值及此时BF的长度.若不存在,请说明理由.
(1)、如图①,Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB边上任意一点,则CD的最小值为 .(2)、如图②,矩形ABCD中,AB=3,BC=4,点M、点N分别在BD、BC上,求CM+MN的最小值.(3)、如图③,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是BC边上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG、CG,四边形AGCD的面积是否存在最小值,若存在,求这个最小值及此时BF的长度.若不存在,请说明理由.