辽宁省沈阳市铁西区2019届九年级数学中考模拟试卷

试卷更新日期：2019-04-12 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $- \frac{2}{7} + (- \frac{5}{7})$ 的正确结果是（）

A、 $\frac{3}{7}$ B、- $\frac{3}{7}$ C、1 D、﹣1

查看试题解析
2. 将3x（a﹣b）﹣9y（b﹣a）因式分解，应提的公因式是（　　）

A、3x﹣9y B、3x+9y C、a﹣b D、3（a﹣b）

查看试题解析
3. 如图所示的圆柱体从正面看得到的图形可能是（）

A、 B、 C、 D、

查看试题解析
4. 我县人口约为530060人，用科学记数法可表示为（）

A、53006×10人 B、5.3006×10⁵人 C、53×10⁴人 D、0.53×10⁶人

查看试题解析
5. 某区“引进人才”招聘考试分笔试和面试．其中笔试按60%、面试按40%计算加权平均数作为总成绩．吴老师笔试成绩为90分．面试成绩为85分，那么吴老师的总成绩为（）分．

A、85 B、86 C、87 D、88

查看试题解析
6. 在平面直角坐标系中，点A（a，0），点B（2﹣a，0），且A在B的左边，点C（1，﹣1），连接AC，BC，若在AB，BC，AC所围成区域内（含边界），横坐标和纵坐标都为整数的点的个数为4个，那么a的取值范围为（）

A、﹣1＜a≤0 B、0≤a＜1 C、﹣1＜a＜1 D、﹣2＜a＜2

查看试题解析
7. 如图，在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别为R、S，若AQ＝PQ，PR＝PS，①PA平分∠BAC；②AS＝AR；③QP∥AR；④△BRP≌△CSP．则这四个结论中正确的有（）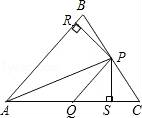

A、4个 B、3个 C、2个 D、1个

查看试题解析
8. 方程 $\frac{2}{x + 2} = \frac{1}{x - 1}$ 解是（）

A、x= $\frac{4}{3}$ B、x=4 C、x=3 D、x=-4

查看试题解析
9. 已知反比例函数y= $\frac{k}{x}$ 的图象经过点P（﹣2，3），则下列各点也在这个函数图象的是（）

A、（﹣1，﹣6） B、（1，6） C、（3，﹣2） D、（3，2）

查看试题解析
10. 二次函数的图象如图所示，对称轴为x=1，给出下列结论：①abc<0；②b²>4ac；③4a+2b+c<0；④2a+b=0..其中正确的结论有：

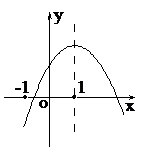A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 计算：（6x⁴﹣8x³）÷（﹣2x²）＝．

查看试题解析
12. 小林同学对甲、乙、丙三个市场某月份每天的白菜价格进行调查，计算后发现这个月三个市场的价格平均值相同，方差分别为S_甲²＝7.5，S_乙²＝1.5，S_丙²＝3.1，那么该月份白菜价格最稳定的是市场．

查看试题解析
13. 已知关于x的一元二次方程x²+bx+1＝0有两个相等的实数根，则b的值为．

查看试题解析
14. 如图，已知AB∥CF，E为DF的中点，若AB=8，CF=5，则BD= ．

查看试题解析
15. 已知关于x的不等式组 ${\begin{cases} 5 - 2 x \geq - 1, \\ x - a > 0 \end{cases}$ 有5个整数解，则a的取值范围是。

查看试题解析
16. 如图，在平面直角坐标系中，矩形OABC的顶点A、C的坐标分别为（10，0），（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为．

查看试题解析

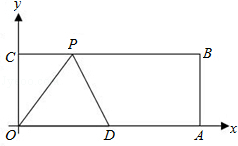
三、解答题

17. 已知x，y满足方程组 ${\begin{matrix} x - 2 y = - 5 \\ 2 x + y = 0 \end{matrix}$ ，求代数式（x﹣y）²﹣（x+2y）（x﹣2y）的值．

查看试题解析
18. 如图，在 $Δ A B C$ 中，AD是高，E、F分别是AB、AC的中点，

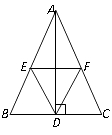(1)、AB＝10，AC＝8，求四边形AEDF的周长；

(2)、EF与AD有怎样的位置关系，证明你的结论．

查看试题解析
19. 不透明的袋中装有3个大小相同的小球，其中两个为白色，一个为红色，随机地从袋中摸取一个小球后放回，再随机地摸取一个小球，（用列表或树形图求下列事件的概率）

(1)、两次取的小球都是红球的概率；

(2)、两次取的小球是一红一白的概率．

查看试题解析
20. 2017年3月27日是全国中小学生安全教育日，某校为加强学生的安全意识，组织了全校学生参加安全知识竞赛，从中抽取了部分学生成绩（得分取正整致，满分为10分）进行统计，绘制了图中两幅不完整的统计图．

(1)、a= ， n=；

(2)、补全频数直方图；

(3)、该校共有2000名学生．若成绩在70分以下（含70分）的学生安全意识不强，有待进一步加强安全教育，则该校安全意识不强的学生约有多少人？

查看试题解析
21. 某商场用2700元购进甲、乙两种商品共100件，这两种商品的进价、标价如下表所示：

(1)、求购进两种商品各多少件？

(2)、商品将两种商品全部卖出后，获得的利润是多少元？

查看试题解析
22. 如图，在平行四边形ABCD中，以A为圆心，AB的长为半径的圆恰好与CD相切于点C，交AD于点E，延长BA与⊙A相交于点F．若弧EF的长为 $\frac{π}{2}$ ，求图中阴影部分的面积．

查看试题解析
23. 如图，Rt△AOB 在平面直角坐标系中，点O与坐标原点重合，点A在x轴上，点B在y轴上， $O B = 2 \sqrt{3} ， A O = 6$ ，将△AOB沿直线BE折叠，使得OB边落在AB上，点O与点D重合.

(1)、求直线BE的解析式；

(2)、求点D的坐标；

(3)、x轴上是否存在点P，使△PAD为等腰三角形？若存在，请直接写出点P的坐标，若不存在，请说明理由。

查看试题解析
24. 点P是矩形ABCD对角线AC所在直线上的一个动点（点P不与点A，C重合），分别过点A，C向直线BP作垂线，垂足分别为点E，F，点O为AC的中点．

(1)、如图1，当点P与点O重合时，请你判断OE与OF的数量关系；

(2)、当点P运动到如图2所示位置时，请你在图2中补全图形并通过证明判断（1）中的结论是否仍然成立；

(3)、若点P在射线OA上运动，恰好使得∠OEF＝30°时，猜想此时线段CF，AE，OE之间有怎样的数量关系，直接写出结论不必证明．

查看试题解析
25. 如图，抛物线 $y = - x^{2} - 2 x + 3$ 的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点.

(1)、求A、B、C的坐标；

(2)、点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N.若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积；

(3)、在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ.过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）.若FG=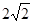 DQ，求点F的坐标.

查看试题解析