湖北省武汉市2019届九年级数学复习调研创优卷（二）

试卷更新日期：2019-04-12 类型：中考模拟

进入出卷网下载

一、单选题

1. 在数轴上，把表示-4的点移动1个单位长度后，所得到的对应点表示的数为（）

A、-2 B、-6 C、-3或-5 D、无法确定

查看试题解析
2. 无论x取什么数，总有意义的分式是 $($ $)$

A、 $\frac{4 x}{x^{3} + 1}$ B、 $\frac{x}{{(x + 1)}^{2}}$ C、 $\frac{3 x}{x^{2} + 1}$ D、 $\frac{x - 2}{x^{2}}$

查看试题解析
3. 已知一个多项式与3x²+9x的和等于5x²+4x﹣1，则这个多项式是（）

A、8x²+13x﹣1 B、﹣2x²+5x+1 C、8x²﹣5x+1 D、2x²﹣5x﹣1

查看试题解析
4. 社会主义核心价值观知识竞赛成绩结果统计如下表：成绩在91---100分的为优胜者，则优胜者的频率是（）

A、35% B、30% C、20% D、10%

查看试题解析
5. 下列运算中，正确的是（）

A、 ${(- \frac{1}{2})}^{- 1} = - 2$ B、 $a^{3} \cdot a^{6} = a^{18}$ C、 $6 a^{6} \div 3 a^{2} = 2 a^{3}$ D、 ${(- 2 a b^{2})}^{2} = 2 a^{2} b^{4}$

查看试题解析
6. 小莹和小博士下棋，小莹执圆子，小博士执方子．如图，棋盘中心方子的位置用（﹣1，0）表示，右下角方子的位置用（0，﹣1）表示．小莹将第4枚圆子放入棋盘后，所有棋子构成一个轴对称图形．她放的位置是（）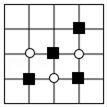

A、（﹣2，1） B、（﹣1，1） C、（1，﹣2） D、（﹣1，﹣2）

查看试题解析
7. 如图所示零件的左视图是（）

A、 B、 C、 D、

查看试题解析
8. 某校在“爱护地球，绿化祖国”的创建活动中，组织了100名学生开展植树造林活动，其植树情况整理如下表：

则这100名学生所植树棵树的中位数为（）

A、4 B、5 C、5.5 D、6

查看试题解析
9. 如图，AB是半圆O的直径，点D在半圆O上，AB= $2 \sqrt{61}$ ，AD=10，C是弧BD上的一个动点，连接AC，过D点作DH⊥AC于H，连接BH，在点C移动的过程中，BH的最小值是（）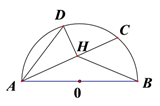

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

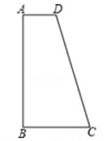
10. 计算： $\sqrt{\frac{1}{6}} \times \sqrt{96} \div \sqrt{6} =$ ．

查看试题解析
11. 化简 $\frac{1}{x - 1}$ ÷ $\frac{1}{x^{2} - 1}$ = ．

查看试题解析
12. 抛掷两枚均匀的正方体骰子（它们的六个面分别标有数字1，2，3，4，5，6），骰子朝上的面的数字分别为 $a ， b$ ，则 $a + b = 6$ 的概率为．

查看试题解析
13. 如图，在四边形 $A B C D$ 中， $∠ B A D = ∠ A B C = 90^{\circ}$ ， $A B = 7$ ， $A D = 2$ ， $B C = 3$ ，若在线段 $A B$ 上取一点 $P$ ，使得以 $P 、 A 、 D$ 为顶点的三角形和以 $P 、 B 、 C$ 为顶点的三角形相似，则这样的 $P$ 点有个．

查看试题解析
14. 等腰△ABC的底边BC=8cm，腰长AB=5cm，一动点P在底边上从点B开始向点C以0.25cm/秒的速度运动，当点P运动到PA与腰垂直的位置时，点P运动的时间应为秒．

查看试题解析
15. 已知 $m 、 n$ 均为整数，当 $x \geq 0$ 时， $(m x + 6) (x + n) \leq 0$ 恒成立，则 $m + n =$ ．

查看试题解析

三、解答题

16. 解方程组： ${\begin{matrix} 4 x - 3 y = 1 \\ 6 x - 4 y = - 2 \end{matrix}$ ．

查看试题解析
17. 如图，在 $Δ A B C$ 中， $A D ⊥ B C$ ，垂足为 $D$ ， $A D = C D$ ，点 $E$ 在 $A D$ 上， $D E = B D$ ， $M 、 N$ 分别是 $A B 、 C E$ 的中点，求 $∠ M D N$ 的度数．

查看试题解析
18. 甲、乙两人5场10次投篮命中次数如图：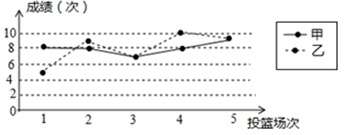

(1)、根据图形填表：

(2)、①教练根据这5个成绩，选择甲参加投篮比赛，理由是什么？
②如果乙再投篮1场，命中8次，那么乙的投篮成绩的方差将会怎样变化？（“变大”“变小”或“不变”）

查看试题解析
19. 某校两次购买足球和篮球的支出情况如表：

(1)、求购买一个足球、一个篮球的花费各需多少元？（请列方程组求解）

(2)、学校准备给帮扶的贫困学校送足球、篮球共计60个，恰逢市场对两种球的价格进行了调整，足球售价提高了10%，篮球售价降低了10%，如果要求一次性购得这批球的总费用不超过4000元，那么最多可以购买多少个足球？

查看试题解析
20. 如图，已知 $Δ B A C ， A B = A C ， O$ 为 $Δ A B C$ 外心， $D$ 为 $⊙ O$ 上一点， $B D$ 与 $A C$ 的交点为 $E$ ，且 $B C^{2} = A C \cdot C E$ ．

(1)、求证： $C D = C B$ ；

(2)、若 $∠ A = 30^{0}$ ，且 $⊙ O$ 的半径为 $3 + \sqrt{3}$ ， $I$ 为 $Δ B C D$ 内心，求 $O I$ 的长．

查看试题解析
21. 如图，点 $A (m ， m + 1) ， B (m + 3 ， m - 1)$ 都在反比例函数 $y = \frac{k}{x}$ 的图象上．

(1)、求 $m ， k$ 的值；

(2)、如果 $M$ 为 $x$ 轴上一点， $N$ 为 $y$ 轴上一点，以点 $A ， B ， M ， N$ 为顶点的四边形是平行四边形，试求直线 $M N$ 的函数表达式；

(3)、将线段 $A B$ 沿直线 $y = k x + b$ 进行对折得到线段 $A_{1} B_{1}$ ，且点 $A_{1}$ 始终在直线 $O A$ 上，当线段 $A_{1} B_{1}$ 与 $x$ 轴有交点时，则 $b$ 的取值范围为（直接写出答案）

查看试题解析
22. 如图，在 $R t Δ A B C$ 中， $∠ B A C = 90^{0}$ ， $A B = A C$ ，点 $D$ 为 $A B$ 延长线上一点，连接 $C D$ ，过 $A$ 分别作 $A M ⊥ C D$ ，垂足为 $M$ ，交 $B C$ 于点 $N$ ，作 $A P ⊥ B C$ ，垂足为 $P$ ，交 $C D$ 于点 $Q$ ．

(1)、求证： $A N = C Q$ ；

(2)、如图，点 $E$ 在 $B A$ 的延长线上，且 $A E = B D$ ，连接 $E N$ 并延长交 $C D$ 于点 $F$ ，求证： $D Q = E N$ ；

(3)、在（2）的条件下，当 $A E = \frac{2}{3} A B$ 时，请直接写出 $\frac{E N}{F N}$ 的值为．

查看试题解析
23. 如图，抛物线y=ax²+bx+c经过A（﹣1，0），B（4，0），C（0，3）三点，D为直线BC上方抛物线上一动点，DE⊥BC于E．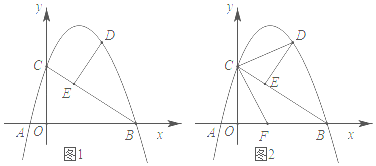

(1)、求抛物线的函数表达式；

(2)、如图1，求线段DE长度的最大值；

(3)、如图2，设AB的中点为F，连接CD，CF，是否存在点D，使得△CDE中有一个角与∠CFO相等？若存在，求点D的横坐标；若不存在，请说明理由．

查看试题解析