2018-2019学年初中数学浙教版八年级下册第四章平行四边形 章末检测
试卷更新日期：2019-04-12 类型：单元试卷
一、选择题
-
1. 下列四种图案中，不是中心对称图形的为（ ）A、
中国移动
B、
中国联通
C、
中国网通
D、
中国电信
2. 利用反证法证明“直角三角形至少有一个锐角不小于45°”，应先假设（ ）A、直角三角形的每个锐角都小于45° B、直角三角形有一个锐角大于45° C、直角三角形的每个锐角都大于45° D、直角三角形有一个锐角小于45°3. 如图，在平行四边形ABCD中，CE⊥AB，E为垂足．如果∠A＝118°，则∠BCE＝（ ）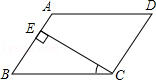
A、28° B、38° C、62° D、72°4. 如图，∠1，∠2，∠3是五边形ABCDE的3个外角，若∠A+∠B＝220°，则∠1+∠2+∠3＝（ ）
A、140° B、180° C、220° D、320°5. 一个多边形的边数增加1，则内角和与外角和增加的度数之和是（ ）A、60° B、90° C、180° D、360°6. 从六边形的一个顶点出发，可以画出m条对角线，它们将六边形分成n个三角形．则m、n的值分别为（ ）A、4，3 B、3，3 C、3，4 D、4，47. 如图，在四边形ABCD中，∠C＝90°，E，F分别为AB，AD的中点，BC＝2，CD＝ ，则EF的长为（ ）
A、 B、 C、 D、8. 已知四边形ABCD，对角线AC与BD交于点O，从下列条件中：①AB∥CD；②AD＝BC；③∠ABC＝∠ADC；④OA＝OC，任取其中两个，以下组合能够判定四边形ABCD是平行四边形的是（ ）A、①② B、②③ C、②④ D、①④9. ▱ABCD中，AD＝8，∠BAD的平分线交BC于E，∠ADC的平分线交BC于F，且EF＝2，则AB的长是（ ）A、5 B、3 C、3或5 D、2或310. 如图，在▱ABCD中，AE⊥BC于E，AF⊥CD于F，若AE＝2，AF＝3，▱ABCD的周长为20，则▱ABCD的面积为（ ）
A、24 B、16 C、8 D、12二、填空题
-
11. 如图所示，在平行四边形ABCD中，DE平分∠ADC交BC于E，AF⊥DE，垂足为F，已知∠DAF＝50°，则∠C的度数是 ．
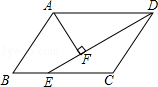12. △ABC与▱DEFG按如图方式放置，点D、G分别在边AB、AC上，点E、F分别在边BC上，若BE＝DE，CF＝FG，则∠A的大小为度．
13. 如图，在平行四边形ABCD中，AB＝8，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且点F为边DC的中点，DG⊥AE，垂足为G，若DG＝3，则AE的边长为 ．
14. 如图，△ABC中，AB＝7cm，BC＝6cm，AC＝5cm，D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长等于cm．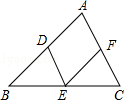
15. 如图，点O是▱ABCD的对称中心，AD＞AB，点E、F在边AB上，且AB＝2EF，点G、H在边BC边上，且BC＝3GH，则△EOF和△GOH的面积比为 ．
16. 如图是由相同的花盆按一定的规律组成的正多边形图案，其中第1个图形一共有6个花盆，第2个图形一共有12个花盆，第3个图形一共有20个花盆，…，则第n个图形中花盆的个数为 ．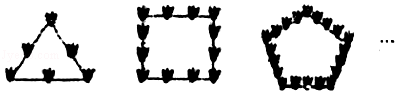
17. 如图，四边形ABCD中，AD∥BC，AD＝8cm，BC＝12cm，M是BC上一点，且BM＝9cm，点E从点A出发以1cm/s的速度向点D运动，点F从点C出发，以3cm/s的速度向点B运动，当其中一点到达终点，另一点也随之停止，设运动时间为t，则当以A、M、E、F为顶点的四边形是平行四边形时，t＝ ．
18. 如图所示，在△ABC中，AB＝AC，D，E分别是AB，AC的中点，G，H为BC上的点连接DH，EG．若AB＝5cm，BC＝6cm，GH＝3cm，则图中阴影部分的面积为 ．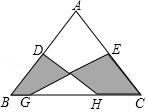
三、解答题
-
19. 用反证法证明（填空）：
两条直线被第三条直线所截．如果同旁内角互补，那么这两条直线平行．
已知：如图，直线l1 ， l2被l3所截，∠1+∠2＝180°．
求证：l1∥l2
证明：假设l1l2 ， 即l1与l2交与相交于一点P．
则∠1+∠2+∠P180°
所以∠1+∠2180°，这与矛盾，故不成立．
所以 ．
20. 如图，以BC为底边的等腰△ABC，点D，E，G分别在BC，AB，AC上，且EG∥BC，DE∥AC，延长GE至点F，使得BE＝BF．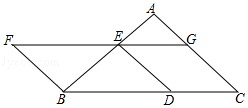
(1)、求证：四边形BDEF为平行四边形；(2)、当∠C＝45°，BD＝2时，求D，F两点间的距离．21. 知识背景：过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分．
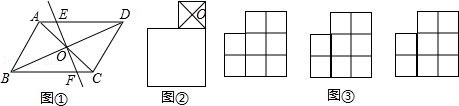(1)、如图①，直线m经过平行四边形ABCD对角线的交点O，则S四边形AEFBS四边形DEFC（填“＞”“＜”“＝”）；(2)、如图②，两个正方形如图所示摆放，O为小正方形对角线的交点，求作过点O的直线将整个图形分成面积相等的两部分；(3)、八个大小相同的正方形如图③所示摆放，求作直线将整个图形分成面积相等的两部分（用三种方法分分割）．22. 已知：如图，在▱ABCD中，对角线AC，BD相交于点O，点E，F在AC上，点G，H在BD上，且AE＝CF，BG＝DH．
(1)、若AC＝6，BD＝8，试求AD的取值范围；(2)、若AC＝AD，∠CAD＝50°，试求∠ABC的度数；(3)、求证：四边形EHFG是平行四边形．23. 如图，在Rt△ABC中，∠B＝90°，AC＝60cm，∠A＝60°，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是ts（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．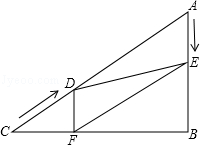
(1)、求证：四边形AEFD是平行四边形；(2)、当t为何值时，△DEF为直角三角形？请说明理由．24. 小明家准备装修厨房，打算铺设如图1的正方形地砖，该地砖既是轴对称图形也是中心对称图形，铺设效果如图2所示．经测量图1发现，砖面上四个小正方形的边长都是4cm，AB＝JN＝2cm，中间的多边形CDEFGHIK是正八边形．
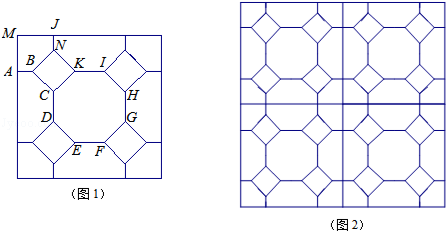(1)、求MA的长度；(2)、求正八边形CDEFGHIK的面积；(3)、已知小明家厨房的地面是边长为3.14米的正方形，用该地砖铺设完毕后，最多形成多少个正八边形？（地砖间缝隙的宽度忽略不计）25. 在平行四边形ABCD中，∠ABE＝45°，点E在对角线AC上，BE的延长线交CD于点F，交AD的延长线于点G，过点C作CH⊥AB于点H，交BF于点M．
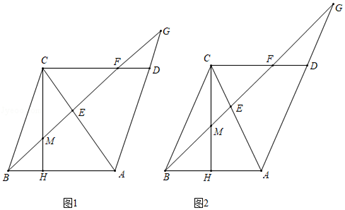(1)、若BE＝3 ，AE＝ ，求△ABE的面积；(2)、若∠ABC＝3∠EBC．CA＝CB，求证：CM＝FG．