广东省云浮市云安区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期：2019-04-12 类型：期末考试
一、选择题（共30分）
-
1. 下面图形中，是中心对称图形的是（ ）A、
B、
C、
D、
2. “抛一枚均匀硬币，落地后正面朝上”这一事件是（ ）
A、随机事件 B、确定事件 C、必然事件 D、不可能事件3. 在平面直角坐标系中，点P(-3，4)关于原点对称的点的坐标是（ ）A、(3，4) B、(3，-4) C、(4，-3) D、(-3，4)4. 抛物线y=(x-1)2+2的顶点坐标是（ ）A、(1，2) B、(-1，2) C、(1，-2) D、(-1，-2)5. 若正六边形外接圆的半径为4，则它的边长为（ ）A、2 B、4 C、4 D、26. 在一个不透明的袋子中，装有红球，黄球，蓝球，白球各1个，这些球除了颜色外无其他区别，从袋中随机取出一个球，取出红球的概率为（ ）A、 B、 C、 D、17. 若关于x的一元二次方程x2-2x+m=0没有实数根，则实数m的取值是（ ）A、m<1 B、m>1 C、m>-1 D、m<-18. 有x支球队参加篮球比赛，共比赛了45场，每两队之间都比赛一场，则下列方程中正确的是（ ）
A、 x(x-1)=45 B、 x(x+1)=45 C、x(x-1)=45 D、x(x+1)=459. 如图，AB是⊙O的直径，弦CD⊥AB于点E．若AB=8，AE=1，则弦CD的长是（ ）
A、 B、2 C、6 D、810. 当ab>0时，y=ax2与y=ax+b的图象大致是（ ）A、
B、
C、
D、
二、填空题（共24分）
-
11. 方程(x-1)(x+2)=0的解是 ．12. ⊙O是△ABC的外接圆，∠BOC=100°，则∠A的度数为 ．13. 将抛物线y=5x2向左平移2个单位得到新的抛物线，则新抛物线的解析式是 ．14. 从甲、乙、丙、丁4名学生中随机抽取2名学生担任数学小组长，则抽取到甲和乙概率为 ．15. 如图，在△ABC中，∠BAC=60°，将△ABC绕着点A顺时针旋转40°后得到△ADE，则∠BAE= ．
16. 如图，在△ABC中，BC=4，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，点P是⊙A上的一点，且∠EPF=45°，则图中阴影部分的面积为 ．
三、解答题（一）（共18分）
-
17. 解一元二次方程：4x2=4x-1．18. 如图，在Rt△ABC中，∠ACB=90°，△DCE是△ABC绕着点C顺时针方向旋转得到的，此时B、C、E在同一直线上．
(1)、旋转角的大小；(2)、若AB=10，AC=8，求BE的长．19. 如图，在Rt△ABC中，∠C=90°，∠B=30°．
(1)、用直尺和圆规作⊙O，使圆心O在BC边，且⊙O经过A，B两点上(不写作法，保留作图痕迹)；(2)、连接A0，求证：AO平分∠CAB．四、解答题（二）（共21分）
-
20. 车辆经过礐石大桥收费站时，在4个收费通道A、B、C、D中，可随机选择其中的一个通过．(1)、一辆车经过此收费站时，选择A通道通过的概率是；(2)、用画树状图或列表的方法，求两辆车经过此收费站时，选择不同通道通过的概率．21. 有一个人患了流感，经过两轮传染后共有81人患了流感．(1)、每轮传染中平均一个人传染了几个人?(2)、按照这样的速度传染，第三轮将又有多少人被传染?22. 如图，有一座拱桥是圆弧形，它的跨度AB=60米，拱高PD=18米．
(1)、求圆弧所在的圆的半径r的长；(2)、当洪水泛滥到跨度只有30米时，要采取紧急措施，若拱顶离水面只有4米，即PE=4米时，是否要采取紧急措施？五、解答题（三）（共27分）
-
23. 4件同型号的产品中，有1件不合格品和3件合格品．
(1)、从这4件产品中随机抽取1件进行检测，求抽到的是不合格品的概率；
(2)、从这4件产品中随机抽取2件进行检测，求抽到的都是合格品的概率；
(3)、在这4件产品中加入x件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，则可以推算出x的值大约是多少？24. 如图，AB是⊙O的直径，点C、D在⊙O上，且AD平分∠CAB，过点D作AC的垂线，与AC的延长线相交于E，与AB的延长线相交于点F，G为AB的下半圆弧的中点，DG交AB于H，连接DB、GB．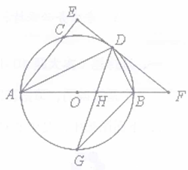
(1)、证明EF是⊙O的切线；(2)、求证：∠DGB=∠BDF：(3)、已知圆的半径R=5，BH=3，求GH的长．25. 如图，抛物线y= x2+bx-2与x轴交于A、B两点，与y轴交于C点，且A(-1，0)．
(1)、求抛物线的解析式及顶点D的坐标；(2)、判断△ABC的形状，证明你的结论；(3)、点M是抛物线对称轴上的一个动点，当△ACM周长最小时，求点M的坐标及△ACM的最小周长．