广东省云浮市云安区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-04-12 类型：期末考试

进入出卷网下载

一、选择题（共30分）

1. 下面四个手机应用图标中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算中正确的是（）

A、a²·a³=a⁵ B、(a²)³=a⁵ C、a⁶÷a²=a³ D、a⁵+a⁵=2a¹⁰

查看试题解析
3. 下列长度的三条线段能组成三角形的是（）

A、 $2, 3, 5$ B、 $7, 4, 2$ C、 $3, 4, 8$ D、 $3, 3, 4$

查看试题解析
4. 下列各分式中，是最简分式的是（）

A、 $\frac{x^{2} + y^{2}}{x + y}$ B、 $\frac{x^{2} - y^{2}}{x + y}$ C、 $\frac{x^{2} + x}{x y}$ D、 $\frac{x y}{y^{2}}$

查看试题解析
5. 在平面直角坐标系 $x O y$ 中，点 $P$ （2，1）关于y轴对称的点的坐标是（）.

A、（－2 ，0 ） B、（－2 ，1 ） C、（－2 ，－1） D、（2 ，－1）

查看试题解析
6. 已知下图中的两个三角形全等，则∠1等于（）

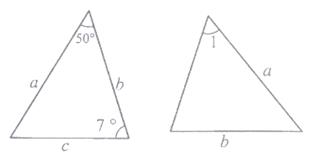A、72° B、60° C、50° D、58°

查看试题解析
7. 如果把 $\frac{5 x}{x + y}$ 中的x与y都扩大为原来的10倍，那么这个代数式的值（）

A、扩大为原来的10倍 B、扩大为原来的5倍 C、缩小为原来的 $\frac{1}{2}$ D、不变

查看试题解析
8. 如果x²+2mx+9是一个完全平方式，则m的值是（）

A、3 B、±3 C、6 D、±6

查看试题解析
9. 为了帮助遭受自然灾害的地区重建家园，某学校号召同学们自愿捐款．已知第一次捐款总额为4800元，第二次捐款总额为5000元，第二次捐款人数比第一次多20人，而且两次人均捐款额恰好相等．如果设第一次捐款人数为x人，那么x满足的方程是（）

A、 $\frac{4800}{x} = \frac{5000}{x - 2}$ B、 $\frac{4800}{x} = \frac{5000}{x + 2}$ C、 $\frac{4800}{x - 20} = \frac{5000}{x}$ D、 $\frac{4800}{x + 20} = \frac{5000}{x}$

查看试题解析

二、填空题（共24分）

10. 2013年，我国上海和安徽首先发现“H7N9”新型禽流感病毒，此病毒颗粒呈多边形，其中球形病毒的最大直径为 $0.00000012$ 米，这一直径用科学记数法表示为米．

查看试题解析
11. 若分式 $\frac{x - 1}{x + 1}$ 有意义，则x的取值范围是．

查看试题解析
12. 因式分解：x²-y²= ．

查看试题解析
13. 计算: $\frac{3 x}{x - 2} + \frac{x + 4}{2 - x}$ 的结果是．

查看试题解析
14. 已知一个多边形的各内角都等于120°，那么它是边形．

查看试题解析
15. 已知等腰三角形的底角是15°，腰长是8cm，则其腰上的高是cm．

查看试题解析

三、解答题（一）（共18分）

16. 分解因式：12b²-3

查看试题解析
17. 解分式方程： $\frac{4 x}{x - 1} - \frac{1}{1 - x}$ =1

查看试题解析
18. 如图，已知△ABC，∠BAC=90°，

(1)、尺规作图：作∠ABC的平分线交AC于D点(保留作图痕迹，不写作法)

(2)、若∠C=30°，求证：DC=DB．

查看试题解析

四、解答题（二）（共21分）

19.

(1)、运用多项式乘法，计算下列各题：
①(x+2)(x+3)=

②(x+2)(x-3)=

③(x-3)(x-1)=

(2)、若：(x+a)(x+b)=x²+px+q，根据你所发现的规律，直接填空：p= ， q= ． (用含a、b的代数式表示)

查看试题解析
20. 先化简，再求值： $\frac{3 a - 3}{a} \div \frac{a^{2} - 2 a + 1}{a^{2}} - \frac{a}{a - 1}$ ，其中a=2

查看试题解析
21. 如图，在△ABC中，D是BC的中点，DE⊥AB于E，DF⊥AC于点F，且BE=CF．

求证：

(1)、△BED≌△CFD；

(2)、AD平分∠BAC．

查看试题解析

五、解答题（三）（共27分）

22. 某服装店用960元购进一批服装，并以每件46元的价格全部售完．由于服装畅销，服装店又用2220元，再次以比第一次进价多5元的价格购进服装，数量是第一次购进服装的2倍，仍以每件46元的价格出售．

(1)、该服装店第一次购买了此种服装多少件?

(2)、两次出售服装共盈利多少元?

查看试题解析
23. 如图，△ABC是等腰直角三角形，∠C=90°，点D是AB的中点，点E，F分别在BC，AC上，且AF=CE．

(1)、填空：∠A的度数是．

(2)、探究DE与DF的关系，并给出证明．

查看试题解析
24. 阅读材料：把形ax²+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫配方法．配方法的基本形式是完全平方公式的逆写，即a²±2ab+b²=(a±b)² ．请根据阅读材料解决下列问题：

(1)、填空：a²-4a+4= ．

(2)、若a²+2a+b²-6b+10=0，求a+b的值．

(3)、若a、b、C分别是△ABC的三边，且a²+4b²+c²-2ab-6b-2c+4=0，试判断△ABC的形状，并说明理由．

查看试题解析