河北省唐山市乐亭县2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-04-11 类型:期中考试
一、选择题(共48分)
-
1. 已知 ,那么下列式子中一定成立的是( )A、x+y=5 B、2x=3y C、 D、
-
2. 为迎接中考体育加试,小刚和小亮分别统计了自己最近10次跳绳成绩,下列统计中能用来比较两人成绩稳定程度的是( )A、平均数 B、中位数 C、众数 D、方差
-
3. 若关于x的一元二次方程(k﹣1)x2+4x+1=0有实数根,则k的取值范围是( )A、k≤5 B、k≤5,且k≠1 C、k<5,且k≠1 D、k<5
-
4. 一元二次方程y2﹣y﹣ =0配方后可化为( )
A、(y+ )2=1 B、(y﹣ )2=1 C、(y+ )2= D、(y﹣ )2= -
5. 若数据a1、a2、a3的平均数是3,则数据2a1、2a2、2a3的平均数是( )A、2 B、3 C、4 D、6
-
6. 若矩形的长和宽是方程x2﹣7x+12=0的两根,则矩形的对角线长度为( )A、5 B、7 C、8 D、10
-
7. 关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根0,则a值为( )A、1 B、﹣1 C、±1 D、0
-
8. 在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )A、
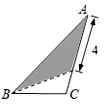 B、
B、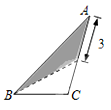 C、
C、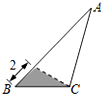 D、
D、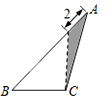
-
9. 如图,点P(x,y)(x>0,y>0)在半径为1的圆上,则cosα=( )
 A、x B、y C、 D、
A、x B、y C、 D、 -
10. 如图,在▱ABCD中,E是AB的中点,EC交BD于点F,则△BEF与△DCB的面积比为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11. 如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为( )
 A、(3,1) B、(3,3) C、(4,4) D、(4,1)
A、(3,1) B、(3,3) C、(4,4) D、(4,1) -
12. 如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
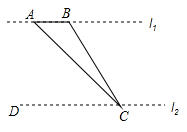 A、50m B、25m C、(50﹣ )m D、(50﹣25 )m
A、50m B、25m C、(50﹣ )m D、(50﹣25 )m -
13. 如图,在▱ABCD中,点E在边AD上,射线CE、BA交于点F,下列等式成立的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14. 如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是 ( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
15. 如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
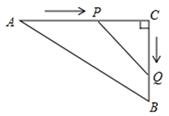 A、5秒 B、20秒 C、5秒或20秒 D、不确定
A、5秒 B、20秒 C、5秒或20秒 D、不确定 -
16. 如图,点A(2,2 ),N(1,0),∠AON=60°,点M为平面直角坐标系内一点,且MO=MA,则MN的最小值为( )
 A、1 B、 C、3 D、2
A、1 B、 C、3 D、2
二、填空题(共12分)
-
17. 若关于x的一元二次方程ax2﹣bx+4=0的解是x=2,则2020+2a﹣b的值是 .
-
18. 一组数据1、2、3、4、5的方差为S12 , 另一组数据6、7、8、9、10的方差为S22 , 那么S12S22(填“>”、“=”或“<”).
-
19. 某商品的利润为每件10元时,能卖500件,已知该商品每涨价1元,其销售量就要减少10件,为了赚8000元利润,设涨价为x元,应列方程为 .
-
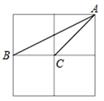
20. 如图,△ABC的三个顶点均在正方形网格格点上,则tan∠BAC= .
三、(本题满分8分)
-
21. 关于x的一元二次方程x2﹣(k+3)x+2k+2=0.(1)、若k=0,求方程的解;(2)、求证:无论k取任何实数时,方程总有两个实数根.
四、(本题满分9分)
-
22. 如图,在8×11网格图中,△ABC与△A1B1C1是位似图形.
 (1)、若在网格上建立平面直角坐标系,使得点A的坐标为(﹣1,6),点C1的坐标为(2,3),则点B的坐标为;(2)、以点A为位似中心,在网格图中作△AB2C2 , 使△AB2C2和△ABC位似,且位似比为1:2;(3)、在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 , 计算四边形ABCP的周长为 .
(1)、若在网格上建立平面直角坐标系,使得点A的坐标为(﹣1,6),点C1的坐标为(2,3),则点B的坐标为;(2)、以点A为位似中心,在网格图中作△AB2C2 , 使△AB2C2和△ABC位似,且位似比为1:2;(3)、在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 , 计算四边形ABCP的周长为 .
五、(本题满分9分)
-
23. 为宣传节约用水,小强随机调查了某小区部分家庭3月份的用水情况,并将收集的数据整理成如下统计图.
 (1)、小强一共调查了户家庭;(2)、求所调查家庭3月份用水量的众数为吨,平均数为吨;(3)、若该小区有800户居民,则该小区3月份的总用水量估计有吨.
(1)、小强一共调查了户家庭;(2)、求所调查家庭3月份用水量的众数为吨,平均数为吨;(3)、若该小区有800户居民,则该小区3月份的总用水量估计有吨.
六、(本题满分10分)
-
24. 某中学连续三年开展植树活动.已知第一年植树500棵,第三年植树720棵,假设该校这两年植树棵数的年平均増长率相同.(1)、求这两年该校植树棵数的年平均增长率;(2)、按照(1)的年平均增长率,预计该校第四年植树多少棵?
七、(本题满分12分)
-
25. 住宅小区有一栋面朝正南的居民楼(如图),该居民楼的一楼高为6米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.已知冬季正午的阳光与水平线的夹角为30°时.
 (1)、新楼的建造对超市以上的居民住房冬季正午的采光是否有影响,为什么?(2)、若要使超市冬季正午的采光不受影响,新楼应建在相距居民楼至少多少米的地方,为什么?(结果保留整数,参考数据:sin30°≈0.5,cos30°≈0.87,tan30°≈0.58)
(1)、新楼的建造对超市以上的居民住房冬季正午的采光是否有影响,为什么?(2)、若要使超市冬季正午的采光不受影响,新楼应建在相距居民楼至少多少米的地方,为什么?(结果保留整数,参考数据:sin30°≈0.5,cos30°≈0.87,tan30°≈0.58)
八、(本题满分12分)
-
26. 如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
 (1)、求证:△ABE∽△ECD;(2)、求证:AE2=AB•AD;(3)、若AB=1,CD=4,求线段AD,DE的长.
(1)、求证:△ABE∽△ECD;(2)、求证:AE2=AB•AD;(3)、若AB=1,CD=4,求线段AD,DE的长.
