华师大版数学八年级下册第十九章第三节19.3正方形同步练习
试卷更新日期:2015-11-16 类型:同步测试
一、选择题
-
1. 已知四边形ABCD是平行四边形,再从①AB=BC , ②∠ABC=90°,③AC=BD , ④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( ).A、①② B、②③ C、①③ D、②④2. 下列说法中,正确的是( ).A、相等的角一定是对顶角 B、四个角都相等的四边形一定是正方形 C、平行四边形的对角线互相平分 D、矩形的对角线一定垂直3. 下列命题中是假命题的是( ).A、一组对边平行且相等的四边形是平行四边形 B、一组对边相等且有一个角是直角的四边形是矩形 C、一组邻边相等的平行四边形是菱形 D、一组邻边相等的矩形是正方形4. 已知四边形ABCD是平行四边形,下列结论中不正确的有( ).
①当AB=BC时,它是菱形;②当AC⊥BD时,它是菱形;③当∠ABC=90°时,它是矩形;④当AC=BD时,它是正方形.
A、1组 B、2组 C、3组 D、4组5. 四边形ABCD的对角线AC=BD , AC⊥BD , 分别过A、B、C、D作对角线的平行线,所成的四边形EFMN是( ).A、正方形 B、菱形 C、矩形 D、任意四边形6. 如果要证明平行四边形ABCD为正方形,那么我们需要在四边形ABCD是平行四边形的基础上,进一步证明( ).A、AB=AD且AC⊥BD B、AB=AD且AC=BD C、∠A=∠B且AC=BD D、AC和BD互相垂直平分7. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形8.如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D , 交AB于点E , 且BE=BF , 添加一个条件,仍不能证明四边形BECF为正方形的是( ).
 A、BC=AC B、CF⊥BF C、BD=DF D、AC=BF9. 下列说法错误的是( ).A、有一个角为直角的菱形是正方形 B、有一组邻边相等的矩形是正方形 C、对角线相等的菱形是正方形 D、对角线相等且互相垂直的四边形是正方形10. 在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H , 这样得到的四边形EFGH中,是正方形的有( ).A、1个 B、2个 C、4个 D、无穷多个11.
A、BC=AC B、CF⊥BF C、BD=DF D、AC=BF9. 下列说法错误的是( ).A、有一个角为直角的菱形是正方形 B、有一组邻边相等的矩形是正方形 C、对角线相等的菱形是正方形 D、对角线相等且互相垂直的四边形是正方形10. 在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H , 这样得到的四边形EFGH中,是正方形的有( ).A、1个 B、2个 C、4个 D、无穷多个11.如图,四边形ABCD中,AD=DC , ∠ADC=∠ABC=90°,DE⊥AB , 若四边形ABCD面积为16,则DE的长为( ).
 A、3 B、2 C、4 D、812. △ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D , OE⊥AC于E , OF⊥AB于F , 且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( ).A、2cm,2cm,2cm B、3cm,3cm,3cm C、4cm,4cm,4cm D、2cm,3cm,5cm13.
A、3 B、2 C、4 D、812. △ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC于D , OE⊥AC于E , OF⊥AB于F , 且AB=10cm,BC=8cm,AC=6cm,则点O到三边AB、AC、BC的距离为( ).A、2cm,2cm,2cm B、3cm,3cm,3cm C、4cm,4cm,4cm D、2cm,3cm,5cm13.如图,在一个大正方形内,放入三个面积相等的小正方形纸片,这三张纸片盖住的总面积是24平方厘米,且未盖住的面积比小正方形面积的四分之一还少3平方厘米,则大正方形的面积是(单位:平方厘米)( )
 A、40 B、25 C、26 D、3614.
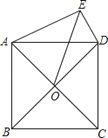
A、40 B、25 C、26 D、3614.如图,正方形ABCD的对角线交于点O , 以AD为边向外作Rt△ADE , ∠AED=90°,连接OE , DE=6,OE= ,则另一直角边AE的长为( ).
 A、 B、2 C、8 D、1015.
A、 B、2 C、8 D、1015.如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD , DP⊥AB于P . 若四边形ABCD的面积是18,则DP的长是( ).
 A、
A、 B、2
C、
D、18
B、2
C、
D、18
二、填空题
-
16. 能使平行四边形ABCD为正方形的条件是(填一个符合题目要求的条件即可).17.
如图,在Rt△ABC中,∠C=90°,DE垂直平分AC , DF⊥BC , 当△ABC满足条件时,四边形DECF是正方形.(要求:①不再添加任何辅助线,②只需填一个符合要求的条件)
 18.
18.如图,菱形ABCD的对角线相交于点O , 请你添加一个条件: , 使得该菱形为正方形.
 19.
19.如图,在四边形ABCD中,AB=BC=CD=DA , 对角线AC与BD相交于点O , 若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加一个条件是
 20. 已知四边形ABCD中,∠A=∠B=∠C=90°,若添加一个条件即可判定该四边形是正方形,那么这个条件可以是
20. 已知四边形ABCD中,∠A=∠B=∠C=90°,若添加一个条件即可判定该四边形是正方形,那么这个条件可以是三、综合题
-
21.
已知:如图,△ABC中,∠ABC=90°,BD是∠ABC的平分线,DE⊥AB于点E , DF⊥BC于点F . 求证:四边形DEBF是正方形.
 22.
22.如图,在四边形ABCD中,AB=BC , 对角线BD平分∠ABC , P是BD上一点,过点P作PM⊥AD , PN⊥CD , 垂足分别为M , N .
 (1)、求证:∠ADB=∠CDB;
(1)、求证:∠ADB=∠CDB;
(2)、若∠ADC=90°,求证:四边形MPND是正方形.23.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB , D为AB边上一点,过点D作DE⊥BC , 交直线MN于E , 垂足为F , 连CD、BE .
 (1)、求证:CE=AD;
(1)、求证:CE=AD;
(2)、当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)、若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

