新华师大版数学八年级上册第十一章第二节11.2实数同步练习
试卷更新日期:2015-11-13 类型:同步测试
一、选择题
-
1. 在实数0、π、 、 、 中,无理数的个数有( )A、1个 B、2个 C、3个 D、4个2. 估计 的值在( )A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间3. ﹣64的立方根与 的平方根之和是( )A、﹣7 B、﹣1或﹣7 C、﹣13或5 D、54. 如图,数轴上A , B两点表示的数分别为﹣1和 ,点B关于点A的对称点为C , 则点C所表示的数为( )
 A、
A、 B、
C、
D、
5. 化简| ﹣π|﹣π得( )A、 B、﹣ C、2π﹣ D、 ﹣2π6. 有下列说法:
B、
C、
D、
5. 化简| ﹣π|﹣π得( )A、 B、﹣ C、2π﹣ D、 ﹣2π6. 有下列说法:①被开方数开方开不尽的数是无理数;②无理数是无限不循环小数;
③无理数包括正无理数、零、负无理数;④无理数都可以用数轴上的点来表示.
其中正确的说法的个数是( )
A、1 B、2 C、3 D、47. 若0<x<1,则x , x2 , , 中,最小的数是( )A、x B、 C、 D、 x28. 若 的整数部分为a , 小数部分为b , 则a﹣b的值为( )A、 B、2 C、2﹣ D、2+9. 的值为( )A、5 B、 C、1
D、
10. 如图,数轴上的A、B、C、D四点中,与数 表示的点最接近的是( )
C、1
D、
10. 如图,数轴上的A、B、C、D四点中,与数 表示的点最接近的是( ) A、点A B、点B C、点C D、点D11. 已知下列结论:①在数轴上的点只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有限个,其中正确的结论是( )A、①② B、②③ C、③④ D、②③④12. 有一个数值转换器原理如图,当输入的x的值为256时,输出的y的值为( )
A、点A B、点B C、点C D、点D11. 已知下列结论:①在数轴上的点只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有限个,其中正确的结论是( )A、①② B、②③ C、③④ D、②③④12. 有一个数值转换器原理如图,当输入的x的值为256时,输出的y的值为( ) A、16 B、 C、 D、13. 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
A、16 B、 C、 D、13. 如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是( ) A、 B、 C、 D、2.514. 任意实数a , 可用[a]表示不超过a的最大整数,如[4]=4,[ ]=1,现对72进行如下操作:72→[ ]=8→[ ]=2→[ ]=1,这样对72只需进行3次操作后变为1.类似地:对数字900进行了n次操作后变为1,那么n的值为( )A、3 B、4 C、5 D、615. 将1、 、 、 按如图方式排列,若规定(m,n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是( )
A、 B、 C、 D、2.514. 任意实数a , 可用[a]表示不超过a的最大整数,如[4]=4,[ ]=1,现对72进行如下操作:72→[ ]=8→[ ]=2→[ ]=1,这样对72只需进行3次操作后变为1.类似地:对数字900进行了n次操作后变为1,那么n的值为( )A、3 B、4 C、5 D、615. 将1、 、 、 按如图方式排列,若规定(m,n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是( )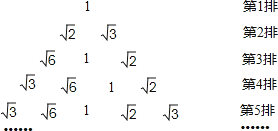 A、 B、6 C、 D、
A、 B、6 C、 D、二、填空题
-
16. 写出一个 到2之间的无理数.17.
下列各数: , , ,1.414, ,3.12122, ,3.161661666…(每两个1之间依次多1个6)中,无理数有个,有理数有个,负数有个,整数有个.
18.在数轴上表示 的点离原点的距离是; 的相反数是 , 绝对值是 .
19.若a1=1,a2= ,a3= ,a4=2,…,按此规律在a1到a2014中,共有无理数个.
20.有下列说法:
①任何无理数都是无限小数;
②有理数与数轴上的点一一对应;
③在1和3之间的无理数有且只有 , , , 这4个;
④ 是分数,它是有理数.
⑤近似数7.30所表示的准确数a的范围是:7.295≤a<7.305.
其中正确的有(填序号).
三、解答题
-
21. 计算:(1)、
 . (2)、
. (2)、 (结果精确到0.01.
(结果精确到0.01.  ). 22. 有一组实数:2, ,0,π, , , ,0.1010010001…(两个1之间依次多个0);(1)、将他们分类,填在相应括号内;
). 22. 有一组实数:2, ,0,π, , , ,0.1010010001…(两个1之间依次多个0);(1)、将他们分类,填在相应括号内;有理数{}
无理数{}
(2)、选出2个有理数和2个无理数,用+,﹣,x,÷中三个不同的运算符号列成一个算式,(可以添括号),使得运算结果为正整数.23. 已知实数x和﹣1.41分别与数轴上的A、B两点对应.(1)、直接写出A、B两点之间的距离(用含x的代数式表示).(2)、求出当x= ﹣1.41时,A、B两点之间的距离(结果精确到0.01).
(3)、若x= ,请你写出大于﹣1.41,且小于x的所有整数,以及2个无理数?
24.如图,4×4方格中每个小正方形的边长都为1.
 (1)、直接写出图1中正方形ABCD的面积及边长;(2)、在图2的4×4方格中,画一个面积为8的格点正方形(四个顶点都在方格的顶点上);并把图(2)中的数轴补充完整,然后用圆规在数轴上表示实数.25.
(1)、直接写出图1中正方形ABCD的面积及边长;(2)、在图2的4×4方格中,画一个面积为8的格点正方形(四个顶点都在方格的顶点上);并把图(2)中的数轴补充完整,然后用圆规在数轴上表示实数.25.阅读下面的文字,解答问题:
大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用 ﹣1来表示 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理,因为 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵ < < ,即2< <3,
∴ 的整数部分为2,小数部分为( ﹣2).
请解答:
(1)、如果 的小数部分为a , 的整数部分为b , 求a+b的值;
(2)、已知:10+ =x+y , 其中x是整数,且0<y<1,求x﹣y的相反数.