江西省南昌市2019届高三理数第一次模拟考试试卷

试卷更新日期：2019-04-09 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $M = {x | x^{2} - 4 〉 0}$ ， $N = {x | {log}_{2} x < 1}$ ，则 $(∁_{R} M) \cap^{} N =$ （）

A、 $\emptyset$ B、 $(0 ， 2)$ C、 $(- 2 ， 2)$ D、 $[- 2 ， 2)$

查看试题解析
2. 已知复数 $z = \frac{a + i}{2 i} (a \in R)$ 的实部等于虚部，则 $a =$ （）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、-1 D、1

查看试题解析
3. 已知抛物线方程为 $x^{2} = - 2 y$ ，则其准线方程为（）

A、 $y = - 1$ B、 $y = 1$ C、 $y = \frac{1}{2}$ D、 $y = - \frac{1}{2}$

查看试题解析
4. 已知 ${a_{n}}$ 为等差数列，若 $a_{2} = 2 a_{3} + 1$ ， $a_{4} = 2 a_{3} + 7$ ，则 $a_{5} =$ （）

A、1 B、2 C、3 D、6

查看试题解析
5. 如图所示算法框图，当输入的 $x$ 为1时，输出的结果为（）

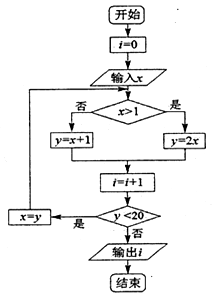A、3 B、4 C、5 D、6

查看试题解析
6. 一个几何体的三视图如图所示，则该几何体的体积为（）

A、 $12 \sqrt{3}$ B、 $14 \sqrt{3}$ C、 $16 \sqrt{3}$ D、 $20 \sqrt{3}$

查看试题解析
7. 2021年广东新高考将实行 $3 + 1 + 2$ 模式，即语文数学英语必选，物理历史二选一，政治地理化学生物四选二，共有12种选课模式.今年高一的小明与小芳都准备选历史，假若他们都对后面四科没有偏好，则他们选课相同的概率（）

A、 $\frac{1}{36}$ B、 $\frac{1}{16}$ C、 $\frac{1}{8}$ D、 $\frac{1}{6}$

查看试题解析
8. 已知 $r > 0$ ， $x ， y \in R$ ， $p$ ：“ $| x | + \frac{| y |}{2} \leq 1$ ”， $q$ ：“ $x^{2} + y^{2} \leq r^{2}$ ”，若 $p$ 是 $q$ 的必要不充分条件，则实数 $r$ 的取值范围是（）

A、 $(0 ， \frac{2 \sqrt{5}}{5}]$ B、 $(0 ， 1]$ C、 $[\frac{2 \sqrt{5}}{5} ， + \infty)$ D、 $[2 ， + \infty)$

查看试题解析
9. 已知 $f (x)$ 在 $R$ 上连续可导， $f^{'} (x)$ 为其导函数，且 $f (x) = e^{x} + e^{- x} - f^{'} (1) x \cdot (e^{x} - e^{- x})$ ，则 $f^{'} (2) + f^{'} (- 2) - f^{'} (0) f^{'} (1) =$ （）

A、 $4 e^{2} + 4 e^{- 2}$ B、 $4 e^{2} - 4 e^{- 2}$ C、0 D、 $4 e^{2}$

查看试题解析
10. 已知平面向量 $\overset{⇀}{a}$ ， $\overset{⇀}{b}$ ， $\overset{⇀}{a} = (2 cos α ， 2 sin α)$ ， $\overset{⇀}{b} = (cos β ， sin β)$ ，若对任意的实数 $λ$ ， $| \overset{⇀}{a} - λ \overset{⇀}{b} |$ 的最小值为 $\sqrt{3}$ ，则此时 $| \overset{⇀}{a} - \overset{⇀}{b} | =$ （）

A、1 B、2 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
11. 已知 $A (- \sqrt{3} ， 0)$ ， $B (\sqrt{3} ， 0)$ ， $P$ 为圆 $x^{2} + y^{2} = 1$ 上的动点， $\overset{⇀}{A P} = \overset{⇀}{P Q}$ ，过点 $P$ 作与 $A P$ 垂直的直线 $l$ 交直线 $Q B$ 于点 $M$ ，则 $M$ 的横坐标范围是（）

A、 $| x | \geq 1$ B、 $| x | > 1$ C、 $| x | \geq 2$ D、 $| x | \geq \frac{\sqrt{2}}{2}$

查看试题解析
12. 杨辉三角，是二项式系数在三角形中的一种几何排列.在欧洲，这个表叫做帕斯卡三角形，帕斯卡（1623-1662）是在1654年发现这一规律的.我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表，这是我国数学史上的一个伟大成就.如图所示，在“杨辉三角”中，去除所有为1的项，依次构成数列 $2 ， 3 ， 3 ， 4 ， 6 ， 4 ， 5 ， 10 ， 10 ， 5 \dots$ ，则此数列前135项的和为（）

A、 $2^{18} - 53$ B、 $2^{18} - 52$ C、 $2^{17} - 53$ D、 $2^{17} - 52$

查看试题解析

二、填空题

13. 设函数 $f (x) = {\begin{matrix} x^{2} - 2^{x}, (x \leq 0) \\ f (x - 3), (x > 0) \end{matrix}$ ，则 $f (5)$ 的值为．

查看试题解析
14. 侧面为等腰直角三角形的正三棱锥的侧棱与底面所成角的正弦值为．

查看试题解析
15. 已知锐角 $A$ 满足方程 $3 cos A - 8 tan A = 0$ ，则 $cos 2 A =$ ．

查看试题解析
16. 定义在封闭的平面区域 $D$ 内任意两点的距离的最大值称为平面区域 $D$ 的“直径”.已知锐角三角形的三个顶点 $A ， B ， C$ 在半径为1的圆上，且 $∠ B A C = \frac{π}{3}$ ，分别以 $Δ A B C$ 各边为直径向外作三个半圆，这三个半圆和 $Δ A B C$ 构成平面区域 $D$ ，则平面区域 $D$ 的“直径”的最大值是．

查看试题解析

三、解答题

17. 函数 $f (x) = 2 sin (ω x + φ)$ （ $0 < ω < \frac{π}{2}$ ， $| φ | < \frac{π}{2}$ ）的部分图像如下图所示， $A (0 ， \sqrt{3})$ ， $C (2 ， 0)$ ，并且 $A B ∥ x$ 轴.

(1)、求 $ω$ 和 $φ$ 的值；

(2)、求 $cos ∠ A C B$ 的值.

查看试题解析
18. 如图，四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面 $A B C D$ 是菱形， $C C_{1} ⊥$ 底面 $A B C D$ ，且 $∠ B A D = 60^{\circ}$ ， $C D = C C_{1} = 2 C_{1} D_{1} = 4$ ， $E$ 是棱 $B B_{1}$ 的中点.

(1)、求证： $A A_{1} ⊥ B D$ ；

(2)、求二面角 $E - A_{1} C_{1} - C$ 的余弦值.

查看试题解析
19. 市面上有某品牌 $A$ 型和 $B$ 型两种节能灯，假定 $A$ 型节能灯使用寿命都超过5000小时，经销商对 $B$ 型节能灯使用寿命进行了调查统计，得到如下频率分布直方图：

某商家因原店面需要重新装修，需租赁一家新店面进行周转，合约期一年.新店面需安装该品牌节能灯5支（同种型号）即可正常营业.经了解， $A$ 型20瓦和 $B$ 型55瓦的两种节能灯照明效果相当，都适合安装.已知 $A$ 型和 $B$ 型节能灯每支的价格分别为120元、25元，当地商业电价为0.75元/千瓦时，假定该店面正常营业一年的照明时间为3600小时，若正常营业期间灯坏了立即购买同型灯更换.（用频率估计概率）

(1)、若该商家新店面全部安装了 $B$ 型节能灯，求一年内恰好更换了2支灯的概率；

(2)、若只考虑灯的成本和消耗电费，你认为该商家应选择哪种型号的节能灯，请说明理由.

查看试题解析
20. 如图，椭圆 $E$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 与圆 $O$ ： $x^{2} + y^{2} = 1$ 相切，并且椭圆 $E$ 上动点与圆 $O$ 上动点间距离最大值为 $\frac{2 + \sqrt{6}}{2}$ .

(1)、求椭圆 $E$ 的方程；

(2)、过点 $N (1 ， 0)$ 作两条互相垂直的直线 $l_{1}$ ， $l_{2}$ ， $l_{1}$ 与 $E$ 交于 $A ， B$ 两点， $l_{2}$ 与圆 $O$ 的另一交点为 $M$ ，求 $Δ A B M$ 面积的最大值，并求取得最大值时直线 $l_{1}$ 的方程.

查看试题解析
21. 已知函数 $f (x) = e^{x} (- x + ln x + a)$ （ $e$ 为自然对数的底数， $a$ 为常数，并且 $a \leq 1$ ）.

(1)、判断函数 $f (x)$ 在区间 $(1, e)$ 内是否存在极值点，并说明理由；

(2)、若当 $a = ln 2$ 时， $f (x) < k (k \in Z)$ 恒成立，求整数 $k$ 的最小值.

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 ${\begin{matrix} x = 2 + t, \\ y = 1 + \sqrt{3} t \end{matrix}$ （ $t$ 为参数），曲线 $C$ 的参数方程为 ${\begin{matrix} x = 4 + 2 c o s θ \\ y = 3 + 2 s i n θ \end{matrix}$ （ $θ$ 为参数），以坐标原点为极点， $x$ 轴非负半轴为极轴建立极坐标系.

(1)、求 $C$ 的极坐标方程；

(2)、设点 $M (2, 1)$ ，直线 $l$ 与曲线 $C$ 相交于点 $A, B$ ，求 $| M A | \cdot | M B |$ 的值.

查看试题解析
23. 已知函数 $f (x) = | x + m^{2} | + | x - 2 m - 3 |$ .

(1)、求证： $f (x) \geq 2$ ；

(2)、若不等式 $f (2) \leq 16$ 恒成立，求实数 $m$ 的取值范围.

查看试题解析