四川省成都市简阳市2018—2019学年九年级上学期数学期末考试试卷

试卷更新日期：2019-04-08 类型：期末考试

进入出卷网下载

一、选择题（A卷）

1. 某几何体的三视图如图所示，则这个几何体是（）

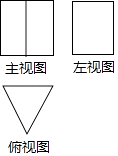A、圆柱 B、长方体 C、三棱锥 D、三棱柱

查看试题解析
2. 要使方程(a-3)x²+(b+1)x+c=0是关于x的一元二次方程，则（）

A、a≠0 B、a≠3 C、a≠3且b≠-1 D、a≠3且b≠-1且c≠0

查看试题解析
3. 如图，白炽灯下有一个乒乓球，当乒乓球越接近灯泡时，它在地面上的影子（）

A、越大 B、越小 C、不变 D、无法确定

查看试题解析
4. 如图，正方形ABCD的边长为1，点E，F分别是对角线AC上的两点，EG⊥AB．EI⊥AD，FH⊥AB，FJ⊥AD，垂足分别为G，I，H，J．则图中阴影部分的面积等于（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
5. 下列各选项的两个图形中，不是位似图形的是（）

A、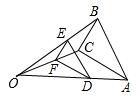 B、 C、 D、

查看试题解析
6. 正方形具有而菱形不一定具有的特征是（）

A、对角线互相垂直平分 B、内角和为360° C、对角线相等 D、对角线平分内角

查看试题解析
7. 在一个布袋里装着只有颜色不同，其他都相同的红、黄、黑三种小球各一个，从中任意摸出一个球；记下颜色后放回并搅匀，再摸出一个球，两次摸球所有可能的结果如图，则摸出的两个球中，一个是红球，一个是黑球的概率是（）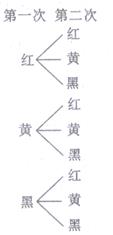

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{1}{3}$ D、 $\frac{4}{9}$

查看试题解析
8. 关于x的一元二次方程kx²+2x-1=0有两个不相等实数根，则k的取值范围是（）

A、k>-1 B、k≥-1 C、k≠0 D、k>-1且k≠0

查看试题解析
9. 如图，在△ABC中，点D在BC边上，连接AD，点G在线段AD上，GE∥BD，且交AB于点E，GF∥AC，且交CD于点F，则下列结论一定正确的是（）.

A、 $\frac{AB}{AE} = \frac{AG}{AD}$ B、 $\frac{DF}{CF} = \frac{DG}{AD}$ C、 $\frac{FG}{AC} = \frac{EG}{BD}$ D、 $\frac{AE}{BE} = \frac{CF}{DF}$

查看试题解析
10. 对于反比例函数y= $\frac{2}{x}$ ，下列说法不正确的起（）

A、点(-2，-1)在它的图象上 B、它的图象在第一、三象限 C、当x>0时，y随x的增大而增大 D、当x<0时，y随x的增大而减小

查看试题解析

二、填空题（A卷）

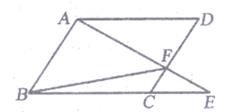
11. 平行四边形、菱形、矩形、正方形的关系是：． (请用文字或图形直观表述)

查看试题解析
12. 鸡蛋孵化小鸡后，小鸡为雌与雄的概率相同，如果两个鸡蛋都成功孵化，则孵出的两只小鸡中都为雄鸡的概率为

查看试题解析
13. 如图所示，点E是平行四边形ABCD的边BC延长线上一点，连接AE，交CD于点F，连接BF．写出图中任意一对相似三角形：．

查看试题解析
14. 关于x的方程mx²+x-m+1=0，有以下三个结论：①当m=0时，方程只有一个实数解；②当m≠0时，方程有两个不相等的实数解；③无论m取何值，方程都有一个负数解．其中正确的是(填序号)．

查看试题解析

三、解答题（A卷）

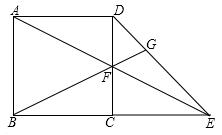
15.

(1)、解方程：x²=x+56

(2)、已知 $\frac{a}{b} = \frac{2}{3}$ ，求 $\frac{a}{a - 2 b}$ 的值

查看试题解析
16. 如图，E，F是正方形ABCD的对角线AC上的两点，且AE=CF．

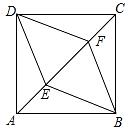(1)、求证：四边形BEDF是菱形；

(2)、若正方形ABCD的边长为4，AE= $\sqrt{2}$ ，求菱形BEDF的面积．

查看试题解析
17. 如图，已知反比例函数y= $\frac{k}{x}$ (x>o)的图象与一次函数y=- $\frac{1}{2}$ x+4的图象交于A和B(6，n)两点．

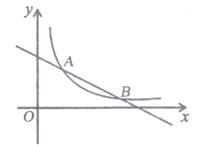(1)、求k和n的值

(2)、若点C(x，y)也在反比例函数y= $\frac{k}{x}$ (x>0)的图象上，求当2≤x≤6时，函数值y的取值范围．

查看试题解析
18. 已知2+ $\sqrt{3}$ 是方程x²-4x+c=0的一个根，求方程的另一个根及c的值．

查看试题解析
19. 为强化已实施的“农村留守儿童关爱计划”，某校对全校各班留守儿童的人数情况进行统计，发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名，共六种情况，并制成了如图的两幅不完整的统计图．

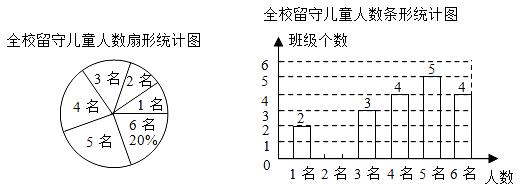(1)、求该校平均每班有多少名留守儿童?并将该条形统计图补充完整．

(2)、某爱心人士决定从只有2名留守儿童的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名留守儿童来自同一个班级的概率。

查看试题解析
20. 刘徽，公元3世纪人，是中国历史上最杰出的数学家之一．《九章算术注》和《海岛算经》是他留给后世最宝贵的数学遗产．
《海岛算经》第一个问题的大意是：如图，要测量海岛上一座山峰A的高度AH，立两根高3丈的标杆BC和DE，两杆之间的距离BD=1000步，D、B、H成一线；从BC退行123步到F，人的眼睛贴着地面观察A点，A、C、F三点成一线；从DE退行127步到G，从G观察A点，A、E、G三点也成一线。试计算山峰的高度AH及BH的长(这里古制1步=6尺，1里=180丈=1800尺=300步，结果用步来表示)．

查看试题解析

四、填空题（B卷）

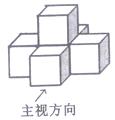
21. 如图是由6个大小相同的立方体组成的几何体，在这个几何体的三视图①主视图、②左视图、③俯视图中，是中心对称图形的有。

查看试题解析
22. 已知0是关于x的方程mx²+5x+m²-2m=0的根，则m= ．

查看试题解析
23. 已知如图，ABCD为矩形，E为对角线AC的中点，A、B在x轴上．若函数y= $\frac{4}{x}$ (x>0)的图象过D、E两点，则矩形ABCD的面积为

查看试题解析
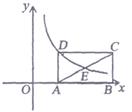24. 设O是四边形ABCD的对角线AC、BD的交点，若∠BAD+∠ACB=180°，且BC=3，AD=4，AC=5，AB=6．则 $\frac{D O}{O B}$ = ．

查看试题解析
25. 如图，菱形ABCD与矩形BNDM有公共的对角线BD，M，N在AC上，且AC=2BD，则DA：MD= ．

查看试题解析

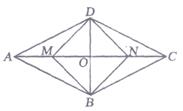
五、解答题（B卷）

26. 在图中，每个正方形由边长为1的小正方形组成：

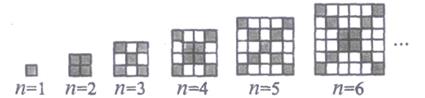(1)、观察图形，请填写下列表格：
正方形边长
1
3
5
7
…
n(奇数)
黑色小正方形的个数

…

正方形边长
2
4
6
8
…
n(偶数)
黑色小正方形的个数

…

(2)、在边长为n(n≥1)的正方形中，设黑色小正方形的个数为p₁ ，白色小正方形的个数为p₂ ，问是否存在偶数n，使p₂=5p₁?若存在，请写出n的值；若不存在，请说明理由．

查看试题解析
27. 已知正方形ABCD的边长是1，E是BC延长线上的一点，CE=1，连接AE，与CD交于F，连接BF并延长与DE交于G，求BG的长．

查看试题解析
28. 如图，已知点D在反比例函数y= $\frac{a}{x}$ 的图象上，过点D作DB⊥y轴，垂足为B(0，3)，直线y=kx+b经过点A(5，0)，与y轴交于点C，且BD=OC，OC：OA=2：5．

(1)、求反比例函数y= $\frac{a}{x}$ 和一次函数y=kx+b的表达式；

(2)、求出关于x的不等式 $\frac{a}{x}$ >kx+b的解集．

查看试题解析

正方形边长	1	3	5	7	…	n(奇数)
黑色小正方形的个数					…

正方形边长	2	4	6	8	…	n(偶数)
黑色小正方形的个数					…