四川省成都市简阳市2018—2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-04-08 类型：期末考试

进入出卷网下载

一、选择题.（A卷）

1. 4的平方根是（）

A、2 B、±2 C、 $\sqrt{2}$ D、± $\sqrt{2}$

查看试题解析
2. 函数y= $\frac{1}{\sqrt{x - 1}}$ 中，自变量x的取值范围是（）

A、x≠1 B、x>0 C、x≥1 D、x>1

查看试题解析
3. 如图，直线a∥b，∠1=60°，则∠2=（）

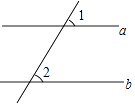A、30° B、60° C、45° D、120°

查看试题解析
4. 如图，以数轴的单位长为边长作一个正方形，以数轴的原点为旋转中心，将过原点的对角线顺时针旋转，使对角线的另一端点落在数轴正半轴的点A处，则点A表示的数是（）

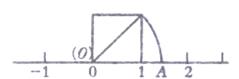A、1 $\frac{1}{2}$ B、1.4 C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
5. 小明为画一个零件的轴截面，以该轴截面底边所在的直线为x轴，对称轴为y轴，建立如图所示的平面直角坐标系．若坐标轴的单位长度取1mm，则图中转折点P的坐标表示正确的是（）

A、（5，30） B、（8，10） C、（9，10） D、（10，10）

查看试题解析
6. 一次函数y=x+2的图象与y轴的交点坐标为（）

A、(0，2) B、(0，-2) C、(2，0) D、(-2，0)

查看试题解析
7. 在“美丽乡村”评选活动中，某乡镇7个村的得分如下：98，90，88，96，92，96，86，这组数据的中位数和众数分别是（）

A、90，96 B、92，96 C、92，98 D、91，92

查看试题解析
8. 二元一次方程组 ${\begin{cases} x + y = 2 \\ 2 x - y = 4 \end{cases}$ 的解是（）

A、 ${\begin{cases} x = 0 \\ y = 2 \end{cases}$ B、 ${\begin{cases} x = 2 \\ y = 0 \end{cases}$ C、 ${\begin{cases} x = 3 \\ y = - 1 \end{cases}$ D、 ${\begin{cases} x = 1 \\ y = 1 \end{cases}$

查看试题解析
9. 如图是甲、乙两位同学5次数学考试成绩的折线统计图，你认为成绩较稳定的是（）．

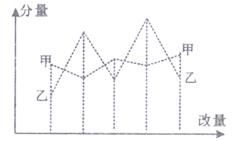A、甲 B、乙 C、甲、乙的成绩一样稳定 D、无法确定

查看试题解析
10. 《九章算术》中记载：“今有共买羊，人出五，不足四十五；人出七，不足三。问人数、羊价各几何?”其大意是：今有人合伙买羊，若每人出5钱，还差45钱；若每人出7钱，还差3钱，问合伙人数、羊价各是多少?设合伙人数为x人，羊价为y钱，根据题意，可列方程组为（）

A、 ${\begin{cases} y = 5 x + 45 \\ y = 7 x + 3 \end{cases}$ B、 ${\begin{cases} y = 5 x - 45 \\ y = 7 x + 3 \end{cases}$ C、 ${\begin{cases} y = 5 x + 45 \\ y = 7 x - 3 \end{cases}$ D、 ${\begin{cases} y = 5 x - 45 \\ y = 7 x - 3 \end{cases}$

查看试题解析

二、填空题（A卷）

11. 下列各数：3.1416， $\frac{21}{21}$ ，0.010010001，3- $π$ ， $0.31 \overset{\cdot}{7}$ ．其中，无理数有个．

查看试题解析
12. 教室里的座位第2排第3列用(2，3)表示，你目前在教室里的座位可以表示为．

查看试题解析
13. 如图，分别以直角三角形的三边为边长向外作正方形，然后分别以三个正方形的中心为圆心，正方形的边长的一半为半径作圆，记三个圆的面积分别为S₁ ， S₂ ， S₃ ，则S₁+S₂S₃ ． (填“>”或“<”或“=”)

查看试题解析
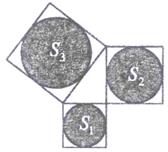14. 若a-3b=-2，3a-b=6，则b-a的值为．

查看试题解析

三、解答题（A卷）

15.

(1)、计算 $\sqrt{18} + {(π - 3.14)}^{0} - 4 \sqrt{\frac{1}{2}}$

(2)、解方程 ${\begin{cases} x = \frac{3 y + 1}{3} \\ 4 x + 3 y = 41 \end{cases}$

查看试题解析
16. 如图，每个小正方形的边长为1，剪一剪，并拼成一个大正方形，

(1)、画出拼成的正方形图形；

(2)、请求这个拼成的正方形的周长．

查看试题解析
17. 为了比较市场上甲、乙两种电子钟每日走时误差的情况，从这两种电子钟
中。各随机抽取10台进行测试，两种电子钟走时误差的数据(单位：s)如下表．

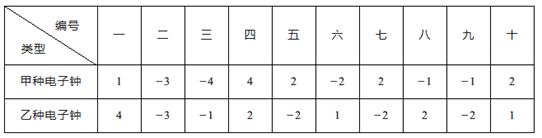(1)、计算甲、乙两种电子钟走时误差的平均数：

(2)、计算甲、乙两种电子钟走时误差的方向：

(3)、根据经验，走时稳定性较好的电子钟质量更优。若两种类型的电子钟价格相同，请问：你买哪种电子钟?为什么?

查看试题解析
18. 已知两直线l₁：y₁=5-x与l₂：y₂=2x-1

(1)、在同一平面直角坐标系中作出两直线的图象；

(2)、求出两直线的交点；

(3)、根据图象指出x为何值时，y₁>y₂；

(4)、求这两条直线与x轴围成的三角形面积．

查看试题解析
19. 勾股定理是一条古老的数学定理。它有很多种证明方法。我国汉代数学家赵爽根据弦图，利用面积法进行证明．著名数学家华罗庚曾提出把“数形关系(勾
股定理)”带到其他星球，作为地球人与其他星球“人”进行第一次“谈话”的语言．

(1)、请你根据图（1）中的直角三角形叙述勾股定理(用文字及符号语言叙述)．

(2)、以图(1)中的直角三角形为基础，可以构造出以a、b为底，以a+b为高的直角梯形（如图（2））。请你利用图（2）证明勾股定理．

查看试题解析
20. 一辆汽车在某次行驶过程中，油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系，其部分图象如图所示。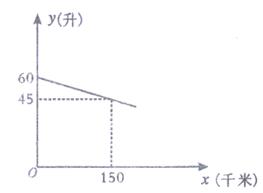

(1)、求y关于x的函数关系式；(不需要写出x的取值范围)

(2)、已知当油箱中的剩余油量为8升时，该汽车会开始提示加油，在此次行驶过程中，行驶了500千米时．司机发现离前方最近的加油站有30千米的路程，在开往该加油站的途中。汽车开始提示加油。这时离加油站的路程是多少千米?

查看试题解析

四、填空题（B卷）

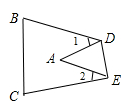
21. 已知直角三角形的周长为2+ $\sqrt{6}$ ，斜边为2，则该三角形的面积是．

查看试题解析
22. 已知点P(2-a，3a-2)到两坐标轴的距离相等，则P点的坐标是．

查看试题解析
23. 已知一次函数y=(-3a+1)x+a的图象上两点A(x₁ ， y₁)、B(x₂ ， y₂)，当x₁>x₂时，有y₁<y₂ ，并且图象不经过第三象限，则a的取值范围是。

查看试题解析
24. 如图，把△ABC沿DE折叠，当点A落在四边形BCED内部时，则∠A与∠1，∠2之间有一种数量关系始终保持不变，请找出这个规律：．

查看试题解析
25. 已知实数a、b、c满足2a+13b+3c=90，3a+9b+c=72，则 $\frac{3 b + c}{a + 2 b}$ = ．

查看试题解析

五、解答题（B卷）

26. 如图，△ABC中，D为BC的中点。DE平分∠ADB，DF平分∠ADC，BE⊥DE，CF⊥DF，P为AD与EF的交点。证明：EF=2PD．

查看试题解析
27. 用若干个形状、大小完全相同的矩形纸片围成正方形，4个矩形纸片围成如
图①所示的正方形，其阴影部分的面积为12；8个矩形纸片围成如图②所示的正方形，其阴影部分的面积为8；12个矩形纸片围成如图③所示的正方形，请求出其阴影部分的面积为多少．

查看试题解析
28. 已知直线y₁=kx+1(k<0)与直线y₂=mx(m>0)的交点坐标为( $\frac{1}{2}$ ， $\frac{1}{2}$ m)，则请求出不等式组mx-2<kx+1<mx的解．

查看试题解析