浙江省宁波市2016-2017学年下学期惠贞书院、鄞州实验、风华书院、邱隘实验4校联考数学试题
试卷更新日期:2017-05-05 类型:中考模拟
一、选择题
-
1. -2的相反数是( )A、2 B、 C、-2 D、2. 雾霾天气对北京地区的人民造成严重影响,为改善大气质量,北京市政府决定投入7600亿元治理雾霾,请你对7600亿元用科学记数法表示( )A、7.6×1010元 B、76×1010元 C、7.6×1011元 D、7.6×1012元3. 抛物线y=3(x-2)2+1的图象先向上平移2个单位,再向左平移2个单位所得的解析式为( )A、y=3x2+3 B、y=3x2-1 C、y=3(x-4)2+3 D、y=3(x-4)2-14. 使得二次根式 有意义的字母 的取值范围是( )A、≥ B、≤ C、< D、≠5. 如图的四个转盘中,C、D转盘分成8等分,若让转盘自由转动一次,停止后,指针落在阴影区域内的概率最大的转盘是( )
A、 B、
B、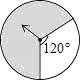 C、
C、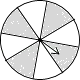 D、
D、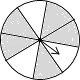 6. 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,则下列等式成立的是( )
6. 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,则下列等式成立的是( ) A、 B、 C、 D、7. 如图是一个机器零件的三视图,根据标注尺寸,这个零件的表面积( )
A、 B、 C、 D、7. 如图是一个机器零件的三视图,根据标注尺寸,这个零件的表面积( ) A、 B、 C、 D、8. 如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到 的位置,使得 ,则 =( )
A、 B、 C、 D、8. 如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到 的位置,使得 ,则 =( ) A、30° B、35° C、40° D、50°9. 一次数学测试后,随机抽取6名学生成绩如下:86,85,88,80,88,95,关于这组数据说法错误的是( )A、方差是20 B、众数是88 C、中位数是86 D、平均数是8710. 如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A、30° B、35° C、40° D、50°9. 一次数学测试后,随机抽取6名学生成绩如下:86,85,88,80,88,95,关于这组数据说法错误的是( )A、方差是20 B、众数是88 C、中位数是86 D、平均数是8710. 如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( ) A、y=2n+1 B、y=2n+n C、y=2n+1+n D、y=2n+n+111. 如图,正方形ABCD中,内部有6个全等的正方形,小正方形的顶点E、F、G、H分
A、y=2n+1 B、y=2n+n C、y=2n+1+n D、y=2n+n+111. 如图,正方形ABCD中,内部有6个全等的正方形,小正方形的顶点E、F、G、H分别在边AD、AB、BC、CD上,则tan∠DEH=( )
 A、 B、 C、 D、12. 如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点,点D是直线BC上方的抛物线上的一个动点,连结DC,DB,则△BCD的面积的最大值是( )
A、 B、 C、 D、12. 如图,抛物线经过A(1,0),B(4,0),C(0,-4)三点,点D是直线BC上方的抛物线上的一个动点,连结DC,DB,则△BCD的面积的最大值是( ) A、7 B、7.5 C、8 D、9
A、7 B、7.5 C、8 D、9二、填空题
-
13. 因式分解: 。14. 若 ,则 的值是。
15. 如图,小明用2m长的标杆测量一棵树的高度.根据图示条件,树高为m. 16. 《九章算术》是我国古代内容极为丰富的数学名著。书中有下列问题“今有勾八步,股十五步。问勾中容圆径几何?”其意思为今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是 步。
16. 《九章算术》是我国古代内容极为丰富的数学名著。书中有下列问题“今有勾八步,股十五步。问勾中容圆径几何?”其意思为今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是 步。
 17. 如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA,OB,使OA=OB;再分别以点A,B为圆心,以大于 AB长为半径作弧,两弧交于点C,若点C的坐标为(m-1,2n),则m与n的关系为m=(用含n的代数式表示)。
17. 如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA,OB,使OA=OB;再分别以点A,B为圆心,以大于 AB长为半径作弧,两弧交于点C,若点C的坐标为(m-1,2n),则m与n的关系为m=(用含n的代数式表示)。 18. 如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线 上,则旋转中心P的坐标为。
18. 如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线 上,则旋转中心P的坐标为。
三、解答题。
-
19. 计算:20. 2017年体育中考在即,学校体育组对九(1)班50名学生进行了长跑项目的测试,根据测试成绩制作了如图两个统计图.

根据统计图解答下列问题:
(1)、本次测试的学生中,得4分的学生有多少人?(2)、本次测试的平均分是多少?(3)、该校九年级共有600名学生参加了长跑项目的测试,估计测试成绩在4分以上(含4分)的人数.21. 综合题。(1)、如图,在图1所给方格纸中,每个小正方形边长都是1,标号为①②③的三个三角形均为格点三角形(顶点在方格顶点处),请按要求将图2中的指定图形分割成三个三角形,使它们与标号为①②③的三个三角形分别对应全等.(分割线画成实线.)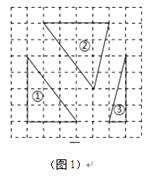
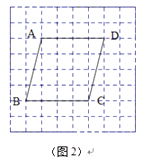 (2)、如图3,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(2)、如图3,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线L成轴对称的 ;
②请直线L上找到一点P,使得PC + PB的距离之和最小.
22. 已知△ABC内接于⊙O , AC是⊙O的直径,D是弧AB的中点.过点D作CB的垂线,分别交CB、CA延长线于点F、E . (1)、判断直线EF与⊙O的位置关系,并说明理由;(2)、若CF=6,∠ACB=60°,求阴影部分的面积.23. 宁波某公司经销一种绿茶,每千克成本为 元.市场调查发现,在一段时间内,销售量 (千克)随销售单价 (元/千克)的变化而变化,具体关系式为: .设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:(1)、求 与 的关系式;(2)、当销售单价 取何值时,销售利润 的值最大,最大值为多少?(3)、如果物价部门规定这种绿茶的销售单价不得高于 元/千克,公司想要在这段时间内获得 元的销售利润,销售单价应定为多少元?24. 请阅读下列材料,并完成相应的任务。
(1)、判断直线EF与⊙O的位置关系,并说明理由;(2)、若CF=6,∠ACB=60°,求阴影部分的面积.23. 宁波某公司经销一种绿茶,每千克成本为 元.市场调查发现,在一段时间内,销售量 (千克)随销售单价 (元/千克)的变化而变化,具体关系式为: .设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:(1)、求 与 的关系式;(2)、当销售单价 取何值时,销售利润 的值最大,最大值为多少?(3)、如果物价部门规定这种绿茶的销售单价不得高于 元/千克,公司想要在这段时间内获得 元的销售利润,销售单价应定为多少元?24. 请阅读下列材料,并完成相应的任务。阿基米德(Archimedes,公元前287~公元前212年,古希腊)是有史以来最伟大的数学家之一.

阿基米德折弦定理:如图1,AB和BC是圆O的两条弦(即折线ABC是圆的一条折弦), BC>AB,M是 的中点,即CD=AB+BD。下面是运用“截长法”证明CD=AB+BD的部分过程。
证明:如图2,在CB上截取CG=AB,连接MA、MB、MC、MG。因为M是弧ABC的中点,所以MA=MC.
任务:
(1)、请按照上面的证明思路,完整证明阿基米德折弦定理,即CD=AB+BD。(2)、如图3,已知等边△ABC内接于圆O,AB=1,D为 上一点,∠ABD=45°,AE⊥BD于点E,则△BDC的周长是.
 25. 如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形.
25. 如果一个三角形能被一条线段分割成两个等腰三角形,那么称这条线段为这个三角形的特异线,称这个三角形为特异三角形. (1)、如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.
(1)、如图1,△ABC中,∠B=2∠C,线段AC的垂直平分线交AC于点D,交BC于点E.求证:AE是△ABC的一条特异线.
(2)、如图2,已知BD是△ABC的一条特异线,其中∠A= ,∠ABC为钝角,求出所有可能的∠ABC的度数.(3)、如图3,△ABC是一个腰长为2的等腰锐角三角形,且它是特异三角形,若它的顶角度数为整数,请求出其特异线的长度;若它的顶角度数不是整数,请直接写出顶角度数.
26. 如图,在平面直角坐标系中,抛物线 与 轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与 轴交于点C(0,-3),顶点为D。 (1)、求抛物线的解析式及顶点D的坐标。(2)、联结AC,BC,求∠ACB的正切值。(3)、点P是x轴上一点,是否存在点P使得△PBD与△CAB相似,若存在,请求出点P的坐标;若不存在,请说明理由。(4)、M是抛物线上一点,点N在 轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由。
(1)、求抛物线的解析式及顶点D的坐标。(2)、联结AC,BC,求∠ACB的正切值。(3)、点P是x轴上一点,是否存在点P使得△PBD与△CAB相似,若存在,请求出点P的坐标;若不存在,请说明理由。(4)、M是抛物线上一点,点N在 轴,是否存在点N,使得以点A,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由。