华师大版数学九年级上册第23章图形的相似23.5位似图形 同步练习
试卷更新日期：2015-11-12 类型：同步测试
一、选择题
-
1. 如图，线段CD两个端点的坐标分别为C（1，2）、D（2，0），以原点为位似中心，将线段CD放大得到线段AB ， 若点B坐标为（5，0），则点A的坐标为（ ）
A、（2，5） B、（2.5，5） C、（3，5） D、（3，6）2. 如图，以点O为位似中心，将△ABC放大得到△DEF.若AD=OA ， 则△ABC与△DEF的面积之比为（ ）
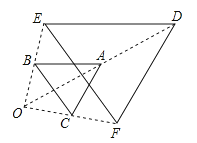A、1：2 B、1：4 C、1：5 D、1：63. 如图，在边长为1的小正方形组成的网格中，建立平面直角坐标系，△ABO与△A′B′O′是以点P为位似中心的位似图形，它们的顶点均在格点（网格线的交点）上，则点P的坐标为（ ）
A、（0，0） B、（0，1） C、（-3，2） D、（3，-2）4.如图，△ABC经过位似变换得到△DEF，点O是位似中心且OA=AD，则△ABC与△DEF的面积比是（ ）
A、1：6 B、1：5 C、1：4 D、1：25.已知，如图，E（-4，2），F（-1，-1）.以O为位似中心，按比例尺1：2把△EFO缩小，点E的对应点的坐标（ ）
A、（-2，1） B、（2，-1） C、（2，-1）或（-2，-1） D、（-2，1）或（2，-1）6. 如图，△DEF与△ABC是位似图形，点O是位似中心，D、E、F分别是OA、OB、OC的中点，则△DEF与△ABC的面积比是（ ）
A、1：6 B、1：5 C、1：4 D、1：27. 如图，已知△ABC，任取一点O，连AO，BO，CO，并取它们的中点D，E，F，得△DEF，则下列说法正确的个数是（ ）①△ABC与△DEF是位似图形； ②△ABC与△DEF是相似图形；
③△ABC与△DEF的周长比为1：2；④△ABC与△DEF的面积比为4：1．
A、1 B、2 C、3 D、48. 如图，线段AB的两个端点坐标分别为A（1，1），B（2，1），以原点O为位似中心，将线段AB放大后得到线段CD.若CD=2，则端点C的坐标为（ ）
A、（2，2） B、（2，4） C、（3，2） D、（4，2）9. 将三角形三个顶点的横坐标都乘以2，纵坐标不变，则所得三角形与原三角形的关系是（ ）A、将原图向左平移两个单位 B、与原点对称 C、纵向不变，横向拉长为原来的二倍 D、关于y轴对称10. 下列说法中：①位似图形一定是相似图形；②相似图形一定是位似图形；③两个位似图形若全等，则位似中心在两个图形之间；④若五边形ABCDE与五边形A′B′C′D′E′位似，则在五边形中连线组成的△ABC与△A′B′C′也是位似的.正确的个数是（ ）A、1 B、2 C、3 D、411. 如图所示，正方形EFGH是由正方形ABCD经过位似变换得到的，点O是位似中心，E ， F ， G ， H分别是OA ， OB ， OC ， OD的中点，则正方形EFGH与正方形ABCD的面积比是（ ）
A、1：6 B、1：5 C、1：4 D、1：212. 如图，菱形ABCD中，对角线AC、BD相交于点O ， M、N分别是边AB、AD的中点，连接OM、ON、MN ， 则下列叙述正确的是（ ）
A、△AOM和△AON都是等边三角形 B、四边形MBON和四边形MODN都是菱形 C、四边形AMON和四边形ABCD都是位似图形 D、四边形MBCO和四边形NDCO都是等腰梯形13. 下列说法正确的是（ ）A、两个位似图形对应点连线有可能无交点 B、两个位似图形对应点连线交点个数为1或2 C、两个位似图形对应点连线只有一个交点 D、两个位似图形对应点连线交点个数不少于4个14. 用作位似形的方法，可以将一个图形放大或缩小，位似中心（ ）A、只能选在原图形的外部 B、只能选在原图形的内部 C、只能选在原图形的边上 D、可以选择任意位置15. 如图，四边形ABCD与四边形AEFG是位似图形，且AC：AF=2：3，则下列结论不正确的是（ ）
A、四边形ABCD与四边形AEFG是相似图形 B、AD与AE的比是2：3 C、四边形ABCD与四边形AEFG的周长比是2：3 D、四边形ABCD与四边形AEFG的面积比是4：9二、填空题
-
16. 坐标系中，△ABC的坐标分别是A（-1，2），B（-2，0），C（-1，1），若以原点O为位似中心，将△ABC放大到原来的2倍得到△A′B′C′，那么落在第四象限的A′的坐标是.17. 直角坐标系中，已知点A（-4，2），B（-2，-2），以原点O为位似中心，把△ABO放大为原来的2倍，则点A的对应点A′的坐标是.18.
△ABC中，点D、E、F分别是AB、BC、AC的中点，则与△ADF位似的三角形是.
19.已知点A（0，1），B（-2，0），以坐标原点O为位似中心，将线段AB放大2倍，放大后的线段A′B′与线段AB在同一侧，则两个端点A′，B′的坐标分别为.
20.将△ABC放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上，ABC的面积等于；
三、综合题
-
21. 在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2，-4），B（3，-2），C（6，-3）.(1)、画出△ABC关于x轴对称的△A1B1C1；
(2)、以M点为位似中心，在网格中画出△A1B1C1的位似图形△A2B2C2 ， 使△A2B2C2与△A1B1C1的相似比为2：1.22.已知点P为线段AB上一点，射线PM⊥AB，用直尺和圆规在PM上找一点C，使得PC2=AP•PB．
23.如图，在平面直角坐标系中，△ABC的三个顶点坐标系分别为A（-2，1），B（-1，4），C（-3，-2）
(1)、以原点O为位似中心，位似比为1：2，在y轴的左侧，画出△ABC放大后的图形△A1B1C1 ， 并直接写出C1点坐标；
(2)、如果点D（a ， b）在线段AB上，请直接写出经过（1）的变化后点D的对应点D1的坐标.
24.如图，在平面直角坐标系中，四边形OABC的顶点坐标分别是O（0，0），A（3，0），B（4，4），C（-2，3），将点O ， A ， B ， C的横坐标、纵坐标都乘以-2.
(1)、画出以变化后的四个点为顶点的四边形；
(2)、由（1）得到的四边形与四边形OABC位似吗？如果位似，指出位似中心及与原图形的相似比.25.如图所示，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′是以点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上.
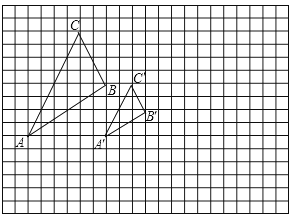(1)、画出位似中心点O；(2)、直接写出△ABC与△A′B′C′的位似比；(3)、以位似中心O为坐标原点，以格线所在直线为坐标轴建立平面直角坐标系，画出△A′B′C′关于点O中心对称的△A″B″C″，并直接写出△A″B″C″各顶点的坐标.