重庆市北碚区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-04-04 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 9的平方根是（   ）
    A、3 B、－3 C、±3 D、± 3

    查看试题解析

  • 2. 计算（-2）100+（-2）99的结果是（   ）
    A、2 B、−2 C、−299 D、299

    查看试题解析

  • 3. 下列多项式乘法中可以用平方差公式计算的是（   ）
    A、(13x+y)(y−13x) B、(x+2)(2+x) C、(−a+b)(a−b) D、(x−2)(x+1)

    查看试题解析

  • 4. 已知a、b、c为△ABC的三边，且满足a2c2-b2c2=a4-b4 ， 则△ABC是（   ）
    A、直角三角形 B、等腰三角形 C、等腰三角形或直角三角形 D、等腰直角三角形

    查看试题解析

  • 5. 下列调查方式，你认为最合适的是（   ）
    A、了解北京市每天的流动人口数，采用抽样调查方式 B、旅客上飞机前的安检，采用抽样调查方式 C、了解北京市居民”一带一路”期间的出行方式，采用全面调查方式 D、日光灯管厂要检测一批灯管的使用寿命，采用全面调查方式

    查看试题解析

  • 6.

    如图，在矩形ABCD中，AC、BD相交于点O，AE平分∠BAD交BC于E，若∠EAO=15°，则∠BOE的度数为（　　）

    A、85°   B、80° C、75° D、70°

    查看试题解析

  • 7. 如图，▱ABCD的对角线 AC ， BD 交于点 O ， AC⊥AB ， AB=5 ，且AC： BD=2 ：3，那么AC的长为（   ）

    A、25 B、5 C、3 D、4

    查看试题解析

  • 8. 如图所示，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（   ）

    A、455 B、235 C、255 D、433

    查看试题解析

  • 9. 如图，在一个高为5m，长为13m的楼梯表面铺地毯，则地毯长度至少应是（   ）

    A、13m B、17m C、18m D、25m

    查看试题解析

  • 10. 如图，在等腰 Δ ABC中，AB=AC，∠BAC=50°，∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合，则∠CEF的度数是（   ）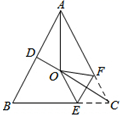

    A、60° B、55° C、50° D、45°

    查看试题解析

  • 11. 如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，有下列结论：①CD=ED；②AC+BE=AB；③∠BDE=∠BAC；④AD平分∠CDE；⑤S△ABD：S△ACD=AB：AC，其中正确的有（   ）

    A、5个 B、4个 C、3个 D、2个

    查看试题解析

二、填空题

  • 12. 若 19  +1的值在两个整数a与a+1之间，则a= ．

    查看试题解析

  • 13. 对于任意实数，规定的意义是 abcd =ad-bc．则当x2-3x+1=0时， x+13xx−2x−1 = ．

    查看试题解析

  • 14. 如图，点P是等边三角形ABC内一点，且PA＝3，PB＝4，PC＝5，若将△APB绕着点B逆时针旋转60度后得到△CQB，则∠APB的度数是 ．

    查看试题解析

  • 15. 有一块田地的形状和尺寸如图所示，则它的面积为。

    查看试题解析

  • 16. 红树林中学共有学生1600人，为了解学生最喜欢的课外体育运动项目的情况，学校随机抽查了200名学生，其中有85名学生表示最喜欢的项目是跳绳，则可估计该校学生中最喜欢的课外体育运动项目为跳绳的学生有人．

    查看试题解析

  • 17. 如图，在平行四边形ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是 ．

    查看试题解析

三、解答题

  • 18.   
    (1)、计算： |−2|+(π−3)0−(13)−2+(−1)2016 ；
    (2)、因式分解：3x2y-18xy2+27y3.

    查看试题解析

  • 19. “食品安全”受到全社会的广泛关注，我区兼善中学对部分学生就食品安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面的两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：

    (1)、接受问卷调查的学生共有多少人，扇形统计图中“基本了解”部分所对应扇形的圆心角为多少度；
    (2)、请补全条形统计图；
    (3)、若对食品安全知识达到“了解”程度的学生中，男、女生的比例恰为2：3，现从中随机抽取2人参加食品安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．

    查看试题解析

  • 20. 正数x的两个平方根分别为3﹣a和2a+7．
    (1)、求a的值；
    (2)、求44﹣x这个数的立方根．

    查看试题解析

  • 21. 如图，∠A=65°，∠ABD=30°，∠ACB=72°，且CE平分∠ACB，求∠BEC的度数．

    查看试题解析

  • 22. 如图，已知AD＝4，CD＝3，BC＝12，AB＝13，∠ADC＝90°，求四边形ABCD的面积．

    查看试题解析

  • 23. 如图，点O是等边△ABC内一点．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．已知∠AOB=110°．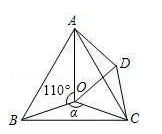

    (1)、求证：△COD是等边三角形；
    (2)、当α=150°时，试判断△AOD的形状，并说明理由；
    (3)、探究：当α为多少度时，△AOD是等腰三角形．

    查看试题解析

  • 24. （题文）图1是一个长为2a，宽为2b的长方形，沿图中虚线剪开分成四块小长方形，然后按图2的形状拼成一个正方形.

       

    (1)、图2的阴影部分的正方形的边长是.
    (2)、用两种不同的方法求图中阴影部分的面积.

    （方法1） S阴影 = ；

    （方法2） S阴影 = ；

    (3)、观察图2，写出(a+b)2 ， (a-b)2 ， ab这三个代数式之间的等量关系；
    (4)、根据 (3) 题中的等量关系，解决问题：若m+n=10，m-n=6，求mn的值.

    查看试题解析

  • 25. 如图1，在 △ABC 中， AE⊥BC 于E， AE=BE ，D是AE上的一点，且 DE=CE ，连接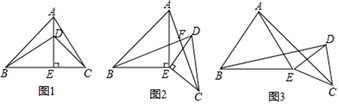BD，CD．

    (1)、试判断BD与AC的位置关系和数量关系，并说明理由；
    (2)、如图2，若将 △DCE 绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；
    (3)、如图3，若将 (2) 中的等腰直角三角形都换成等边三角形，其他条件不变．

    ① 试猜想BD与AC的数量关系，请直接写出结论；

    ② 你能求出BD与AC的夹角度数吗？如果能，请直接写出夹角度数；如果不能，请说明理由．

    查看试题解析