浙江省湖州市吴兴区2018-2019学年八年级上学期期末考试数学试题

试卷更新日期：2019-04-04 类型：期末考试

进入出卷网下载

一、单选题

1. 平面直角坐标系内有一点P（-2019，-2019），则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知线段 $a$ =6cm， $b$ =8cm，则下列线段中，能与 $a$ , $b$ 组成三角形的是（）

A、2cm B、12cm C、14cm D、16cm

查看试题解析
3. 下列四个手机品牌商标中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 若 $x < y$ ，则下列式子不成立的是（）

A、 $x - 1 < y - 1$ B、 $- 2 x < - 2 y$ C、 $x + 3 < y + 3$ D、 $\frac{x}{2} < \frac{y}{2}$

查看试题解析
5. 能说明命题“对于任何实数a，|a|＞﹣a”是假命题的一个反例可以是（）

A、a＝﹣2 B、a＝ $\frac{1}{3}$ C、a＝1 D、a＝ $\sqrt{2}$

查看试题解析
6. 小冬不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1，2，3，4的四块），你认为将其中的哪一块带去，能配一块与原来一样大小的三角形？应该带（）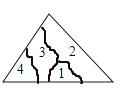

A、第1块 B、第2块 C、第3块 D、第4块

查看试题解析
7. 已知点A（1，y₁），B（-3，y₂）都在直线 $y = - \frac{1}{2} x + 2$ 上，则（）

A、y_1< y₂ B、y₁₌ y₂ C、y₁>y₂ D、不能比较

查看试题解析
8. 已知y=kx+k²（k≠0）的图象与y=-2x的图象平行，则y=kx+k²的大致图象是（）

A、 B、 C、 D、

查看试题解析
9. 如图所示，在△ABC中，AB=AC=5，BC=8.CD是AB边上的高线，则AD的长度为（）

A、 $\frac{12}{5}$ B、 $\frac{24}{5}$ C、 $\frac{13}{5}$ D、 $\frac{7}{5}$

查看试题解析
10. 已知等边△ABC中，在射线BA上有一点D，连接CD，并以CD为边向上作等边△CDE，连接BE和AE.试判断下列结论：①AE=BD； ②AE与AB所夹锐夹角为60°；③当D在线段AB或BA延长线上时，总有∠BDE-∠AED=2∠BDC；④∠BCD=90°时，CE²+AD²=AC²+DE² .正确的序号有（）

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析

二、填空题

11. 在平面直角坐标系中，点A（1， $- 3$ ）关于 $x$ 轴的对称点的坐标为．

查看试题解析
12. 函数 $y = \frac{1}{x - 3}$ 的自变量x的取值范围是．

查看试题解析
13. 同时满足 $\frac{x - 3}{2} > x - 3$ 和 $3 x + 4 > x$ 的最大整数是．

查看试题解析
14. 已知直角三角形两条直角边长为1和 $\sqrt{3}$ ，则此直角三角形斜边上的中线长是．

查看试题解析
15. 如图2，小靓用边长为16的七巧板（如图1）拼成一幅装饰图，放入长方形ABCD内，拼成一个“木马”形状（如图2），图中的三角形顶点E在边CD上，三角形的边AM，GF分别在边AD，BC上，则AB长是．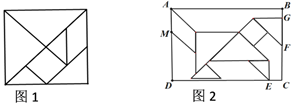

查看试题解析
16. 如图1，△ABC中，沿∠BAC的平分线AB₁折叠，剪掉重叠部分；将余下部分沿∠B₁A₁C的平分线A₁B₂折叠，剪掉重叠部分；…；将余下部分沿∠B_nA_nC的平分线A_nB_n+1折叠，点B_n与点C重合，无论折叠多少次，只要最后一次恰好重合，我们就称∠BAC是△ABC的好角.

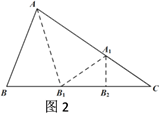(1)、如图2，在△ABC中，∠B>∠C，若经过两次折叠，∠BAC是△ABC的好角，则∠B与∠C的等量关系是；

(2)、如果一个三角形的最小角是20°，则此三角形的最大角为时，该三角形的三个角均是此三角形的好角。

查看试题解析

三、解答题

17. 解下列不等式 $\frac{1 + x}{2} \leq \frac{1 + 2 x}{3} + 1$ ，并把解在数轴上表示出来.

查看试题解析
18. 如图，在△ABC和△DEF中，B、E、C、F在同一直线上，下面有四个条件：
①AB=DE，②AC=DF，③∠ABC=∠DEF，④BE=CF．请你在其中选3个作为题设，余下的1个作为结论，写一个真命题，并加以证明．

查看试题解析
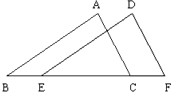19. 如图，在△ABC中，∠B=∠C=60°，AD⊥BC于D，E为AC的中点，CB=8，求DE的长.

查看试题解析
20. 某学校的平面示意图如图所示，实验楼所在位置的坐标为(-2，-3)，教学楼所在位置的坐标为(-1，2)，

(1)、请确定图书馆所在位置的坐标．

(2)、某人在校门位置，请用方向与距离的方法表示实验楼.

(3)、连接图书馆与校门的线段向右平移5个单位，则平移后的线段上任意一点怎样表示？

查看试题解析
21. 如图，是某汽车距离目的地的路程S(千米）与时间t（分钟）的函数关系图.观察图中所提供的信息，解答下列问题：

(1)、汽车在前9分钟内的平均速度是.

(2)、汽车在中途停了多长时间？

(3)、当 $16 \leq t \leq 30$ ，求S关于t的函数关系式.

查看试题解析
22. 小强打算找印刷公司设计一款新年贺卡并印刷.如图1是甲印刷公司设计与印刷卡片计价方式的说明（包含设计费与印刷费），乙公司的收费与印刷卡片数量的关系如图2所示.

(1)、分别写出甲乙两公司的收费y（元）与印刷数量x之间的关系式.

(2)、如果你是小强，你会选择哪家公司？并说明理由.

查看试题解析
23. 在Rt△ABC中，∠ACB=90°，点D与点B在AC同侧，∠DAC＞∠BAC，且DA=DC，过点B作BE∥DA交DC于点E，过E作EM∥AC交AB于点M，连结MD.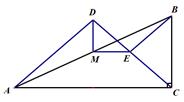

(1)、当∠ADC=80°时，求∠CBE的度数.

(2)、当∠ADC=α时：
①求证：BE=CE.

②求证：∠ADM=∠CDM.

③当α为多少度时，DM= $\sqrt{3}$ EM.

查看试题解析
24. 如图1，在平面直角坐标系中，直线 $l$ ： $y = \frac{3}{4} x + \frac{3}{2}$ 与 $x$ 轴交于点A，且经过点B（2，m），点C（3，0）.

(1)、求直线BC的函数解析式；

(2)、在线段BC上找一点D，使得△ABO与△ABD的面积相等，求出点D的坐标；

(3)、y轴上有一动点P，直线BC上有一动点M，若△APM是以线段AM为斜边的等腰直角三角形，求出点M的坐标；

(4)、如图2，E为线段AC上一点，连结BE，一动点F从点B出发，沿线段BE以每秒1个单位运动到点E，再沿线段EA以每秒 $\sqrt{2}$ 个单位运动到A后停止，设点F在整个运动过程中所用时间为t，求t的最小值.

查看试题解析