江苏省射阳县五校2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-04-04 类型:期末考试
一、单选题
-
1. 下面图形表示绿色食品、节水、节能和低碳四个标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,点M(﹣4,﹣3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列各数:-2,0, ,0.020020002…, , ,其中无理数的个数是( )A、4 B、3 C、2 D、14. 点P到△ABC的三个顶点的距离相等,则点P是△ABC ( )的交点.A、三条高 B、三条角平分线 C、三条中线 D、三边的垂直平分线5. 如图,△ABC中,AB=AC,AB=5,BC=8,AD是∠BAC的平分线,则AD的长为( )
2. 在平面直角坐标系中,点M(﹣4,﹣3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列各数:-2,0, ,0.020020002…, , ,其中无理数的个数是( )A、4 B、3 C、2 D、14. 点P到△ABC的三个顶点的距离相等,则点P是△ABC ( )的交点.A、三条高 B、三条角平分线 C、三条中线 D、三边的垂直平分线5. 如图,△ABC中,AB=AC,AB=5,BC=8,AD是∠BAC的平分线,则AD的长为( )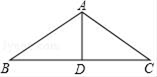 A、5 B、4 C、3 D、26. 如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )
A、5 B、4 C、3 D、26. 如图,∠AOB=30°,OC为∠AOB内部一条射线,点P为射线OC上一点,OP=4,点M、N分别为OA、OB边上动点,则△MNP周长的最小值为( )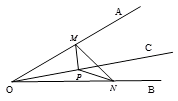 A、2 B、4 C、 D、
A、2 B、4 C、 D、二、填空题
-
7. 的相反数是 .8. 近似数40.6万精确到位.9. 如图,已知∠ABD=∠CBD,若以“SAS”为依据判定△ABD≌△CBD,还需添加的一个条件是 .
 10. 一次函数 的图像不经过第象限.11. 如图,△ABC中,AB=6,∠BAC的平分线交BC于点D,DE⊥AC于点E,DE=4,则△ABD面积是 .
10. 一次函数 的图像不经过第象限.11. 如图,△ABC中,AB=6,∠BAC的平分线交BC于点D,DE⊥AC于点E,DE=4,则△ABD面积是 .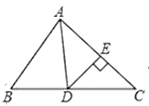 12. 如图,已知函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是 .
12. 如图,已知函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是 . 13. 若点A( ,5)与B(2,5)的距离为5,则 = .14. 在平面直角坐标系中,点A(2,3)绕原点O逆时针旋转90°的对应点的坐标为 .15. 在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于 AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C= .
13. 若点A( ,5)与B(2,5)的距离为5,则 = .14. 在平面直角坐标系中,点A(2,3)绕原点O逆时针旋转90°的对应点的坐标为 .15. 在△ABC中,按以下步骤作图:①分别以A,B为圆心,大于 AB的长为半径画弧,相交于两点M,N;②作直线MN交AC于点D,连接BD.若CD=BC,∠A=35°,则∠C= .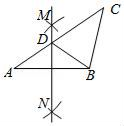 16. 如图, ,若 ,则 = .
16. 如图, ,若 ,则 = .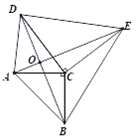
三、解答题
-
17. 计算: +|2﹣ |﹣20140﹣( )-1.18. 若实数 、 满足( )2+ =0,求 的平方根.19. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
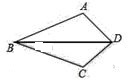
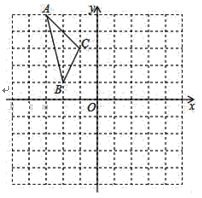 (1)、若△ABC和△A1B1C1关于x轴成轴对称,画出△A1B1C1(2)、点C1的坐标为 , △ABC的面积为.20. 已知:如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.求证:AO=BO.
(1)、若△ABC和△A1B1C1关于x轴成轴对称,画出△A1B1C1(2)、点C1的坐标为 , △ABC的面积为.20. 已知:如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.求证:AO=BO.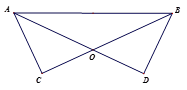 21. 如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,则乙船的航行方向为南偏东多少度?
21. 如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,则乙船的航行方向为南偏东多少度?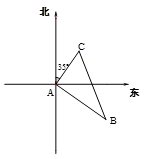 22. 市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品 件( >0),购买两种商品共花费 元.(1)、求出 与 的函数关系式(写出自变量 的取值范围);(2)、试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?23. 如图,点O为线段AD上一点,CO⊥AD于点O,OA=OB,OC=OD,点M、N分别是AC、BD的中点,连接OM、ON、MN.
22. 市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品 件( >0),购买两种商品共花费 元.(1)、求出 与 的函数关系式(写出自变量 的取值范围);(2)、试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?23. 如图,点O为线段AD上一点,CO⊥AD于点O,OA=OB,OC=OD,点M、N分别是AC、BD的中点,连接OM、ON、MN.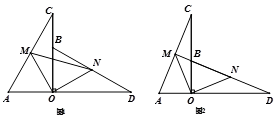 (1)、求证:AC=BD;(2)、试判断△MON的形状,并说明理由;(3)、若AC=2,在图2中,点M在DB的延长线上,求△AMD的面积.24. 甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离 (千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(1)、求证:AC=BD;(2)、试判断△MON的形状,并说明理由;(3)、若AC=2,在图2中,点M在DB的延长线上,求△AMD的面积.24. 甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离 (千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.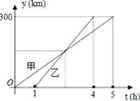 (1)、A,B两城相距千米,乙车比甲车早到小时;(2)、甲车出发多长时间与乙车相遇?(3)、若两车相距不超过20千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?25. 已知长方形ABCD中,AD=10cm,AB=6cm,点M在边CD上,由C往D运动,速度为1cm/s,运动时间为t秒,将△ADM沿着AM翻折至△AD´M,点D对应点为D´,AD´所在直线与边BC交于点P.
(1)、A,B两城相距千米,乙车比甲车早到小时;(2)、甲车出发多长时间与乙车相遇?(3)、若两车相距不超过20千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?25. 已知长方形ABCD中,AD=10cm,AB=6cm,点M在边CD上,由C往D运动,速度为1cm/s,运动时间为t秒,将△ADM沿着AM翻折至△AD´M,点D对应点为D´,AD´所在直线与边BC交于点P.

 (1)、如图1,当t=0时,求证:PA=PC;(2)、如图2,当t为何值时,点D´恰好落在边BC上;(3)、如图3,当t=3时,求CP的长.26. 在平面直角坐标系中,直线l1: 与坐标轴交于A,B两点,直线l2: ( ≠0)与坐标轴交于点C,D.
(1)、如图1,当t=0时,求证:PA=PC;(2)、如图2,当t为何值时,点D´恰好落在边BC上;(3)、如图3,当t=3时,求CP的长.26. 在平面直角坐标系中,直线l1: 与坐标轴交于A,B两点,直线l2: ( ≠0)与坐标轴交于点C,D.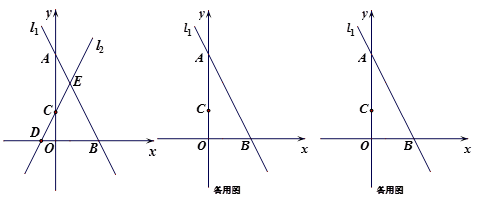 (1)、求点A,B的坐标;(2)、如图,当 =2时,直线l1 , l2与相交于点E,求两条直线与 轴围成的△BDE的面积;(3)、若直线l1 , l2与 轴不能围成三角形,点P(a,b)在直线l2: (k≠0)上,且点P在第一象限.
(1)、求点A,B的坐标;(2)、如图,当 =2时,直线l1 , l2与相交于点E,求两条直线与 轴围成的△BDE的面积;(3)、若直线l1 , l2与 轴不能围成三角形,点P(a,b)在直线l2: (k≠0)上,且点P在第一象限.①求 的值;
②若 ,求 的取值范围.