江苏省南京市建邺区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-04-04 类型:期末考试
一、单选题
-
1. 下列手机手势解锁图案中,是轴对称图形的是( )A、
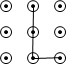 B、
B、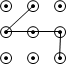 C、
C、 D、
D、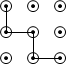 2. 的相反数是( )A、 B、- C、 D、-3. 在平面直角坐标系中,点P(2,-3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列整数中,与 最接近的是( )A、4 B、5 C、6 D、75. 如图,已知AC⊥BD,垂足为O,AO = CO,AB = CD,则可得到△AOB≌△COD,理由是( )
2. 的相反数是( )A、 B、- C、 D、-3. 在平面直角坐标系中,点P(2,-3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 下列整数中,与 最接近的是( )A、4 B、5 C、6 D、75. 如图,已知AC⊥BD,垂足为O,AO = CO,AB = CD,则可得到△AOB≌△COD,理由是( )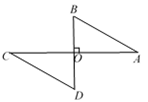 A、HL B、SAS C、ASA D、SSS6. 如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为( )
A、HL B、SAS C、ASA D、SSS6. 如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为( )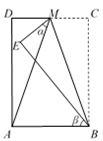 A、α+3β=180° B、β-α=20° C、α+β=80° D、3β-2α=90°
A、α+3β=180° B、β-α=20° C、α+β=80° D、3β-2α=90°二、填空题
-
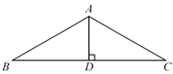
7. 点A(2,-3)关于x轴对称的点的坐标是 .8. 如图,在△ABC中,AB = AC,∠BAC = 120º,AD⊥BC,则∠BAD = .
 9. 如图,△ABC≌△ADE,点E在BC上,若∠C = 80°,则∠DEB = °.
9. 如图,△ABC≌△ADE,点E在BC上,若∠C = 80°,则∠DEB = °. 10. 若一次函数的图象与直线y=-2x平行,且经过点(1,3),则一次函数的表达式为 .11. 有一个数值转换器,原理如下:
10. 若一次函数的图象与直线y=-2x平行,且经过点(1,3),则一次函数的表达式为 .11. 有一个数值转换器,原理如下:
当输入的x = 4时,输出的y等于 .
12. 表1给出了直线l1上部分点(x,y)的坐标值,表2给出了直线l2上部分点(x,y)的坐标值.表1
x
-2
-1
0
1
y
-6
-3
0
3
表2
x
-2
-1
0
1
y
0
-3
-6
-9
那么直线l1和直线l2交点坐标为 .
13. 如图,在△ABC中,∠C = 90°,AC = 8,BC = 6,D点在AC上运动,设AD长为x,△BCD的面积y,则y与x之间的函数表达式为 .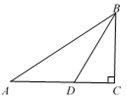 14. 如图,在△ABC中,∠ABC = 90°,AB = 2BC = 2,在AC上截取CD = CB.在AB上截取AP = AD,则AP = .
14. 如图,在△ABC中,∠ABC = 90°,AB = 2BC = 2,在AC上截取CD = CB.在AB上截取AP = AD,则AP = .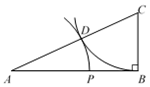 15. 如图,正方形ABCD的三个顶点A、B、D分别在长方形 EFGH的边EF、FG、EH上,且C到HG的距离是1,到点H,G的距离分别为 , ,则正方形ABCD的面积为 .
15. 如图,正方形ABCD的三个顶点A、B、D分别在长方形 EFGH的边EF、FG、EH上,且C到HG的距离是1,到点H,G的距离分别为 , ,则正方形ABCD的面积为 .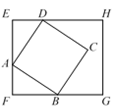 16. 已知A(0,0),B(2,0),C(3,3),如果在平面直角坐标系中存在一点D,使得△ABD与△ABC全等,那么点D的坐标为 .
16. 已知A(0,0),B(2,0),C(3,3),如果在平面直角坐标系中存在一点D,使得△ABD与△ABC全等,那么点D的坐标为 .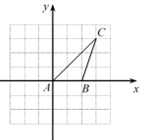
三、解答题
-
17. 求下列各式中x的值:(1)、x2-4 = 0;(2)、(x-3)3 = 8.18. 如图,△ABC ≌ △ADE,∠BAD = 60°.求证:△ACE是等边三角形.
 19. 已知一次函数y =-2x+4,完成下列问题:
19. 已知一次函数y =-2x+4,完成下列问题: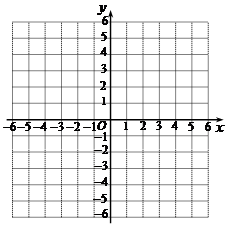 (1)、在所给直角坐标系中画出此函数的图象;(2)、根据图象回答:当x时,y > 2.20. 如图,在平面直角坐标系中,已知A(0,8),B(4,8),C是x轴正半轴上一点,点P满足下面两个条件:①P到∠AOC两边的距离相等;②PA = PB.
(1)、在所给直角坐标系中画出此函数的图象;(2)、根据图象回答:当x时,y > 2.20. 如图,在平面直角坐标系中,已知A(0,8),B(4,8),C是x轴正半轴上一点,点P满足下面两个条件:①P到∠AOC两边的距离相等;②PA = PB. (1)、利用尺规,作出点P的位置(不写作法,保留作图痕迹);(2)、点P的坐标为 .21. 如图,把长为12 cm的纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,且∠FPH = 90°,BF = 3 cm,求FH的长.
(1)、利用尺规,作出点P的位置(不写作法,保留作图痕迹);(2)、点P的坐标为 .21. 如图,把长为12 cm的纸条ABCD沿EF,GH同时折叠,B、C两点恰好落在AD边的P点处,且∠FPH = 90°,BF = 3 cm,求FH的长.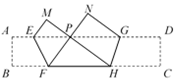 22. 下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,设第x个图案中白色正方形的个数为y.
22. 下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,设第x个图案中白色正方形的个数为y.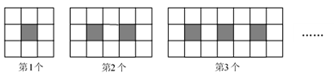 (1)、y与x之间的函数表达式为(直接写出结果).(2)、是否存在这样的图案,使白色正方形的个数为2018个?如果存在,请指出是第几个图案;如果不存在,说明理由.23. 如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.
(1)、y与x之间的函数表达式为(直接写出结果).(2)、是否存在这样的图案,使白色正方形的个数为2018个?如果存在,请指出是第几个图案;如果不存在,说明理由.23. 如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.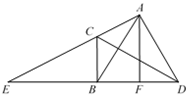
求证:
(1)、AB是∠CAF的角平分线;(2)、∠FAD = ∠E.24. 某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如表:x/元
…
15
20
25
…
y/件
…
25
20
15
…
已知日销售量y是销售价x的一次函数.
(1)、求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;(2)、当每件产品的销售价定为35元时,此时每日的销售利润是多少元?25. 小明从家出发,沿一条直道散步到离家450 m的邮局,经过一段时间原路返回,刚好在第12 min回到家中.设小明出发第t min时的速度为v m/min,v与t之间的函数关系如图所示(图中的空心圈表示不包含这一点).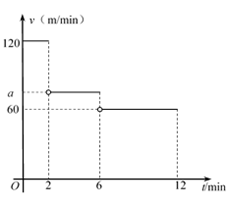 (1)、小明出发第2 min时离家的距离为m;(2)、当2< t ≤6时,求小明的速度a;(3)、求小明到达邮局的时间.26. (数学阅读)如图
(1)、小明出发第2 min时离家的距离为m;(2)、当2< t ≤6时,求小明的速度a;(3)、求小明到达邮局的时间.26. (数学阅读)如图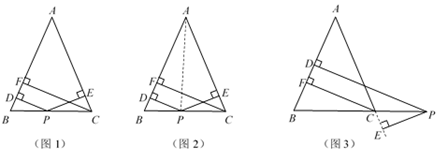
如图1,在△ABC中,AB=AC,点P为边BC上的任意一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F,求证:PD+PE=CF.
小尧的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
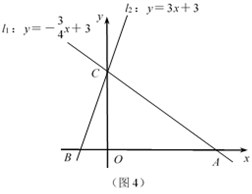
(1)、【推广延伸】如图3,当点P在BC延长线上时,其余条件不变,请运用上述解答中所积累的经验和方法,猜想PD,PE与CF的数量关系,并证明.(2)、【解决问题】如图4,在平面直角坐标系中有两条直线l1:y=- x+3,l2:y=3x+3,l1 , l2与x轴的交点分别为A,B.①两条直线的交点C的坐标为;
②说明△ABC是等腰三角形;
③若l2上的一点M到l1的距离是1,运用上面的结论,求点M的坐标.