湖北省鄂州地区2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2019-04-04 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形：①三角形，②线段，③正方形，④直角、⑤圆，其中是轴对称图形的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
2. 已知点P(a＋1，2a －3)关于x轴的对称点在第一象限，则a的取值范围是（）

A、 $a < - 1$ B、 $- 1 < a < \frac{3}{2}$ C、 $- \frac{3}{2} < a < 1$ D、 $a > \frac{3}{2}$

查看试题解析
3. 下列各式计算正确的是（）

A、 ${(a^{5})}^{2} = a^{7}$ B、 $2 x^{- 2} = \frac{1}{2 x^{2}}$ C、 $3 a^{2} • 2 a^{3} = 6 a^{6}$ D、 $a^{8} \div a^{2} = a^{6}$

查看试题解析
4. 把代数式 $3 x^{3} - 12 x^{2} + 12 x$ 分解因式，结果正确的是（）

A、 $3 x (x^{2} - 4 x + 4)$ B、 $3 x {(x - 4)}^{2}$ C、 $3 x (x + 2) (x - 2)$ D、 $3 x {(x - 2)}^{2}$

查看试题解析
5. 一个多边形的外角和是内角和的 $\frac{2}{5}$ ，这个多边形的边数为（）

A、5 B、6 C、7 D、8

查看试题解析
6. 化简 $(1 - \frac{2 x - 1}{x^{2}}) \div (1 - \frac{1}{x^{2}})$ 的结果为（）

A、 $\frac{x - 1}{x + 1}$ B、 $\frac{x + 1}{x - 1}$ C、 $\frac{x + 1}{x}$ D、 $\frac{x - 1}{x}$

查看试题解析
7. 如图，正△ABC的边长为2，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l对称，D为线段BC′上一动点，则AD＋CD的最小值是（）

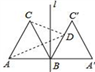A、4 B、3 $\sqrt{2}$ C、2 $\sqrt{3}$ D、2＋ $\sqrt{3}$

查看试题解析
8. 如图，△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线OD交于点O，将∠C沿EF(E在BC上，F在AC上)折叠，点C与点O恰好重合，则∠OEC度数为（）.

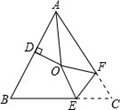A、108° B、135° C、144° D、160°

查看试题解析
9. 若数 $a$ 使关于 $x$ 的分式方程 $\frac{2}{x - 1} + \frac{a}{1 - x} = 4$ 的解为正数，且使关于 $y$ 的不等式组 ${\begin{matrix} \frac{y + 2}{3} - \frac{y}{2} > 1 \\ 2 (y - a) \leq 0 \end{matrix}$ 的解集为 $y < - 2$ ，则符合条件的所有整数 $a$ 的和为（）

A、10 B、12 C、14 D、16

查看试题解析
10. 若关于x的分式方程 $\frac{2 m + x}{x - 3} - 1 = \frac{2}{x}$ 无解，则m的值为（）

A、一l.5 B、1 C、一l.5或2 D、一0.5或一l.5

查看试题解析

二、填空题

11. 细胞扥直径只有1微米，即0.000001米，用科学记数法表示0.00000001为。

查看试题解析
12. 计算： $a^{- 2} b^{2} • {(a^{2} b^{- 2})}^{- 3} \div {(a^{- 4})}^{2}$ =。

查看试题解析
13. 分式方程 $\frac{x}{x - 1} - 1 = \frac{m}{(x - 1) (x + 2)}$ 有增根，则 $m$ 的值为。

查看试题解析
14. 已知 $2^{x} = 3, 2^{y} = 5$ ，则 $2^{2 x - y - 1}$ 的值为。

查看试题解析
15. 如图，折叠直角三角形纸片的直角，使点C落在AB上的点E处，已知BC=24，∠B=30∘，则DE的长是.

查看试题解析
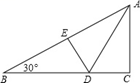16. 如图，△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC，则∠EFC=°.

查看试题解析
17. 如图，在直角坐标系中，点A的坐标是(2，0)，点B的坐标是(0，3)，以AB为腰作等腰三角形，则另一顶点在坐标轴上的有个。

查看试题解析
18. 已知三个数x， y， z，满足 $\frac{x y}{x + y} = - 2 ， \frac{y z}{y + z} = \frac{4}{3} ， \frac{z x}{z + x} = - \frac{4}{3} ，$
则

查看试题解析

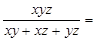
三、解答题

19.

(1)、化简 $[(x + y) (x - y) - {(x - y)}^{2} + 2 y (x - y)] \div (- 2 y)$

(2)、因式分解① $2 m (a - b) - 6 n (b - a)$ ② ${(a - 2 b)}^{2} + 8 a b$

查看试题解析
20. 解方程

(1)、 $\frac{3}{x^{2} - 9} + \frac{x}{x - 3} = 1$

(2)、 $\frac{1}{x + 1} + \frac{2}{x - 1} = \frac{4}{x^{2} - 1}$

查看试题解析
21. 如图，已知△ABC是等边三角形，D为边AC的中点，AE⊥EC，BD=EC．

(1)、求证：△BDA≌△CEA；

(2)、请判断△ADE是什么三角形，并说明理由．

查看试题解析
22. 化简 $\frac{a}{a^{2} - 4} \cdot \frac{a + 2}{a^{2} - 3 a}$ - $\frac{1}{2 - a}$ ，并求值。其中a与2,3分别为△ABC三边长，且a为整数。

查看试题解析
23. 如图，在Rt△ABC中，∠ACB=90∘，AC=BC，点D为BC的中点，CE⊥AD于点E，其延长线交AB于点F，连接DF.求证：∠ADC=∠BDF.

查看试题解析
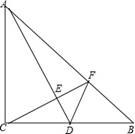24. 某工厂计划在规定时间内生产24 000个零件.若每天比原计划多生产30个零件，则在规定时间内可以多生产300个零件.

(1)、求原计划每天生产的零件个数和规定的天数；

(2)、为了提前完成生产任务，工厂在安排原有工人按原计划正常生产的同时，引进5组机器人生产流水线共同参与零件生产，已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%.按此测算，恰好提前两天完成24 000个零件的生产任务，求原计划安排的工人人数.

查看试题解析
25. 如图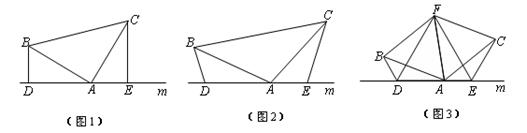

(1)、如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m， CE⊥直线m，垂足分别为点D、E.证明：DE=BD+CE.

(2)、如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC= $α$ ，其中 $α$ 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立，请你给出证明；若不成立，请说明理由.

(3)、拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.

查看试题解析