贵州省安顺地区2018—2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-04-04 类型:期末考试
一、单选题
-
1. 如图,四个图标中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
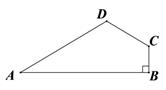
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 已知一粒米的质量是0.000021千克,这个数字用科学记数法表示( )A、 千克 B、 千克 C、 千克 D、 千克4. 如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 已知一粒米的质量是0.000021千克,这个数字用科学记数法表示( )A、 千克 B、 千克 C、 千克 D、 千克4. 如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( ) A、∠B=∠E B、AC=DC C、∠A=∠D D、AB=DE5. 下列各分式中,是最简分式的是( )A、 B、 C、 D、6. 如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC=( )
A、∠B=∠E B、AC=DC C、∠A=∠D D、AB=DE5. 下列各分式中,是最简分式的是( )A、 B、 C、 D、6. 如图,△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC=( )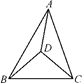 A、100° B、80° C、70° D、50°7. 如图,能根据图形中的面积说明的乘法公式是( )
A、100° B、80° C、70° D、50°7. 如图,能根据图形中的面积说明的乘法公式是( )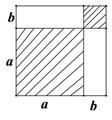 A、 B、 C、 D、8. 已知 为整数,且 为正整数,求所有符合条件的 的值的和( )A、0 B、12 C、10 D、89. 用直尺和圆规作一角的平分线的依据是( )
A、 B、 C、 D、8. 已知 为整数,且 为正整数,求所有符合条件的 的值的和( )A、0 B、12 C、10 D、89. 用直尺和圆规作一角的平分线的依据是( )
A、SSS B、SAS C、ASA D、AAS10. 如图,已知正方形ABCD的边长是为10cm,△ABE为等边三角形(点E在正方形内),若P是AC上的一个动点,PD+PE的最小值是多少( ) A、6cm B、8cm C、10cm D、5cm
A、6cm B、8cm C、10cm D、5cm二、填空题
-
11. 在平面直角坐标系中,点 (-3,4) 关于y轴对称的点的坐标是 .12. 一个正多边形的内角和为540 ,则这个正多边形的每个外角的度数为 .13. 当x时,分式 有意义.14. 甲、乙两个搬运工搬运某种货物.已知乙比甲每小时多搬运600kg,甲搬运5000kg所用的时间与乙搬运8000kg所用的时间相等.设甲每小时搬运x kg货物,则可列方程为 .15. 如图,∠AOB=30°,P是∠AOB的角平分线上的一点,PM⊥OB于点M,PN∥OB交OA于点N,若PM=1,则PN= .
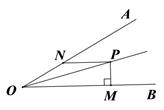 16. 如图,在△ABC中,∠B=40°,∠C=45°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,则∠DAE= .
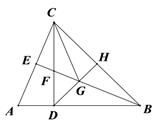
16. 如图,在△ABC中,∠B=40°,∠C=45°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,则∠DAE= . 17. 对于实数 ,b定义一种新运算“ ”: ,例如, .则方程 的解是.18. 如图,D、E、F分别为BC、AD、BE的中点,若△BFD的面积为6,则 △ABC的面积等于.
17. 对于实数 ,b定义一种新运算“ ”: ,例如, .则方程 的解是.18. 如图,D、E、F分别为BC、AD、BE的中点,若△BFD的面积为6,则 △ABC的面积等于.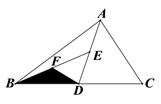
三、解答题
-
19. 计算:(1)、[a(a2b2-ab)-b(-a3b-a2)]÷a2b;(2)、 .20. 因式分解:(1)、 ;(2)、 .21. 先化简 ,然后从 的范围内选取一个合适的整数作为x的值代入求值。