广西河池市2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期：2019-04-04 类型：期末考试
一、单选题
-
1. 世界上最小的鸟是生活在古巴的吸蜜蜂鸟，它的质量约为 盎司 将 用科学记数法表示为A、 B、 C、 D、2. 下列四个汽车标志图中，不是轴对称图形的是（ ）A、
B、
C、
D、
3. 下列因式分解正确的是（ ）A、6x+9y+3=3(2x+3y) B、x2+2x+1=(x+1)2 C、x2-2xy-y2=(x-y)2 D、x2+4=(x+2)24. 若分式 的值为0，则 的值等于（ ）A、0 B、2 C、3 D、-35. 等腰三角形有两条边长为5cm和9cm，则该三角形的周长是（ ）A、18cm B、19cm C、23cm D、19cm或23cm6. 点P（3，4）关于y轴对称的点的坐标是（ ）A、（3，﹣4） B、（﹣3，4） C、（﹣4，﹣3） D、（﹣4，3）7. 如图，小敏用三角尺按下面方法画角平分线：在已知的∠AOB的两边上，分别取OM＝ON，再分别过点M，N作OA，OB的垂线，交点为P，画射线OP，则OP平分∠AOB，其作图原理是：△OMP≌△ONP，这样就有∠AOP＝∠BOP，则说明这两个三角形全等的依据是（ ）
A、SAS B、ASA C、AAS D、HL8. 如图，已知在△ABC，AB＝AC．若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是（ ）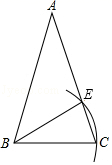
A、AE＝EC B、AE＝BE C、∠EBC＝∠BAC D、∠EBC＝∠ABE9. 计算（x+2）2的结果为x2+□x+4，则“□”中的数为（ ）A、－2 B、2 C、－4 D、410. 如图，在△ABC中，∠B=∠C=60，点D为AB边的中点，DE⊥BC于E ， 若BE=1，则AC的长为（ ）
A、2 B、 C、4 D、11. 已知 =3，则代数式 的值是（ ）A、 B、 C、 D、12. 如图，点P是∠AOB内任意一点，且∠AOB＝40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时，则∠MPN的度数为（ ）
A、140° B、100° C、50° D、40°二、填空题
-
13. 当x时，分式 有意义．14. 计算：6a2b÷2a= ．15. 如图，点B、F、C、E在一条直线上，已知BF=CE，AC∥DF，请你添加一个适当的条件 ， 使得△ABC≌△DEF．
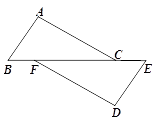16. 各角都相等的十五边形的每个内角的度数是度．17. 如图，若△ACD的周长为50，DE为AB的垂直平分线，则AC+BC＝ ．
18. 如图，在△ABC中，∠ACB＝90°，AD是△ABC的角平分线，BC＝10cm，BD：DC＝3：2，则点D到AB的距离为 ．
三、解答题
-
19. 解分式方程： .20. 因式分解：
（ 1 ）a3b﹣ab3
（ 2 ）（x+1）（x+3）+1
21. 已知：AD是△ABC中BC边上的中线，延长AD至E，使DE＝AD，连接BE，求证：△ACD≌△EBD．
22. 现有三个村庄A，B，C，位置如图所示，线段AB，BC，AC分别是连通两个村庄之间的公路．现要修一个水站P，使水站不仅到村庄A，C的距离相等，并且到公路AB，AC的距离也相等，请在图中作出水站P的位置．（要求：尺规作图，不写作法，保留作图痕迹．）
23. 先化简，再求值：（m+2﹣ ）× ，其中m＝4．24. 列分式方程解应用题：北京第一条地铁线路于1971年1月15日正式开通运营．截至2017年1月，北京地铁共有19条运营线路，覆盖北京市11个辖区．据统计，2017 年地铁每小时客运量是2002年地铁每小时客运量的4倍，2017年客运240万人所用的时间比2002年客运240万人所用的时间少30小时，求2017年地铁每小时的客运量？25. 把一个长为2m，宽为2n的长方形沿图1中的虚线平均分成四块小长方形，然后拼成一个正方形（如图2）
(1)、请用两种不同的方法求图2中阴影部分的面积（直接用含m，n的代数式表示）方法1：
方法2：
(2)、根据（1）中的结论，请你写出代数式（m+n）2 ， （m﹣n）2 ， mn之间的等量关系；(3)、根据（2）中的等量关系，解决如下问题：已知实数a，b满足：a+b＝3，ab＝2，求a﹣b的值．26. 如图，在等边三角形ABC的外侧作直线AP，点C关于直线AP的对称点为点D，连接AD，BD，其中BD交直线AP于点E.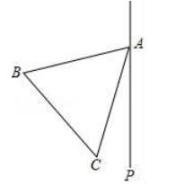
(1)、依题意补全图形；
(2)、若∠PAC＝20°，求∠AEB的度数；
(3)、连结CE，写出AE， BE， CE之间的数量关系，并证明你的结论．