甘肃省兰州市永登县2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-04-04 类型:期末考试
一、单选题
-
1. 在 六个数中,无理数的个数为( )A、4 B、3 C、2 D、12. 下列计算正确的是( )A、2﹣1=﹣2 B、 =±3 C、(ab2)2=a2b4 D、3. 如图,小手盖住的点的坐标可能是( )
 A、(3,3) B、(﹣4,5) C、(﹣4,﹣6) D、(3,﹣6)4. 我市某中学九年级(1)班为开展“阳光体育运动”,决定自筹资金为班级购买体育器材,全班50名同学捐款情况如下表:
A、(3,3) B、(﹣4,5) C、(﹣4,﹣6) D、(3,﹣6)4. 我市某中学九年级(1)班为开展“阳光体育运动”,决定自筹资金为班级购买体育器材,全班50名同学捐款情况如下表:捐款(元)
5
10
15
20
25
30
人数
3
6
11
11
13
6
问该班同学捐款金额的众数和中位数分别是( )
A、13,11 B、25,30 C、20,25 D、25,205. 下列命题中是假命题的是( )A、直角三角形的两个锐角互余 B、对顶角相等 C、两条直线被第三条直线所截,同位角相等 D、三角形任意两边之和大于第三边6. 点P(2,﹣1)关于原点中心对称的点的坐标是( )A、(2,1) B、(﹣2,﹣1) C、(﹣1,2) D、(﹣2,1)7. 一次函数y=(m—1)x+m2的图象过点(0,4),且y随x的增大而增大,则m的值为( )A、-2 B、2 C、1 D、-2或28. 下列各组数中,能构成直角三角形的是( )A、4,5,6 B、1,1, C、6,8,11 D、5,12,239. 正比例函数y=kx(k≠0)的图像经过第二、四象限,则一次函数y=x+k的图像大致是( )A、 B、
B、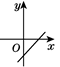 C、
C、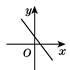 D、
D、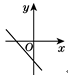 10. 如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( )
10. 如图,已知a∥b,∠1=130°,∠2=90°,则∠3=( ) A、70° B、100° C、140° D、170°11. 如果 a3xby与﹣a2ybx+1是同类项,则( )A、 B、 C、 D、12. 如图,△ABC的角平分线BO、CO相交于点O,∠A=120°,则∠BOC=( )
A、70° B、100° C、140° D、170°11. 如果 a3xby与﹣a2ybx+1是同类项,则( )A、 B、 C、 D、12. 如图,△ABC的角平分线BO、CO相交于点O,∠A=120°,则∠BOC=( ) A、150° B、140° C、130° D、120°13. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≥-2 B、x>-2 C、x≥2 D、x≤214. 如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组 的解是( )
A、150° B、140° C、130° D、120°13. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≥-2 B、x>-2 C、x≥2 D、x≤214. 如图,已知函数y=x+1和y=ax+3图象交于点P,点P的横坐标为1,则关于x,y的方程组 的解是( ) A、 B、 C、 D、15. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )
A、 B、 C、 D、15. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( ) A、小明中途休息用了20分钟 B、小明休息前爬山的平均速度为每分钟70米 C、小明在上述过程中所走的路程为6600米 D、小明休息前爬山的平均速度大于休息后爬山的平均速度
A、小明中途休息用了20分钟 B、小明休息前爬山的平均速度为每分钟70米 C、小明在上述过程中所走的路程为6600米 D、小明休息前爬山的平均速度大于休息后爬山的平均速度二、填空题
-
16. 函数 是y关于x的正比例函数,则 .17. 计算:( )2015( )2016= .18. 如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 cm.
 19. 已知方程组 的解是 ,则a+b的值为 .20. 如图,已知一次函数 的图象为直线,则关于 的方程 的解 .
19. 已知方程组 的解是 ,则a+b的值为 .20. 如图,已知一次函数 的图象为直线,则关于 的方程 的解 .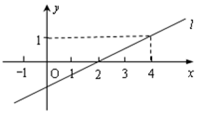
三、解答题
-
21.(1)、(2)、22. 如图,已知:DE⊥AO于点E, BO⊥AO于点O,∠CFB=∠EDO,证明:CF∥DO .
 23. 已知△PQR在直角坐标系中的位置如图所示:
23. 已知△PQR在直角坐标系中的位置如图所示: (1)、求出△PQR的面积;(2)、画出△P′Q′R′,使△P′Q′R′与△PQR关于y轴对称,写出点P′、Q′、R′的坐标;(3)、连接PP′,QQ′,判断四边形QQ′P′P的形状,求出四边形QQ′P′P的面积.24. 如图,直线EF分别与直线AB、CD相交于点M、N,且∠1=∠2,MO、NO分别平分∠BMF和∠END,试判断△MON的形状,并说明理由.
(1)、求出△PQR的面积;(2)、画出△P′Q′R′,使△P′Q′R′与△PQR关于y轴对称,写出点P′、Q′、R′的坐标;(3)、连接PP′,QQ′,判断四边形QQ′P′P的形状,求出四边形QQ′P′P的面积.24. 如图,直线EF分别与直线AB、CD相交于点M、N,且∠1=∠2,MO、NO分别平分∠BMF和∠END,试判断△MON的形状,并说明理由. 25. 学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2 , 且它们的函数图象如图所示,根据图象信息,请你回答下列问题:
25. 学校准备五一组织老师去隆中参加诸葛亮文化节,现有甲、乙两家旅行社表示对老师优惠,设参加文化节的老师有x人,甲、乙两家旅行社实际收费为y1、y2 , 且它们的函数图象如图所示,根据图象信息,请你回答下列问题: (1)、当参加老师的人数为多少时,两家旅行社收费相同?(2)、求出y1、y2关于x的函数关系式?(3)、如果共有50人参加时,选择哪家旅行社合算?26. 某校办工厂有工人60名,生产某种由一个螺栓套两个螺母的配套产品,每人每天平均生产螺栓14个或螺母20个,应分配多少人生产螺栓,多少人生产螺母,能使生产出的螺栓和螺母刚好配套?27. 为了解我市的空气质量情况,某环保兴趣小组从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
(1)、当参加老师的人数为多少时,两家旅行社收费相同?(2)、求出y1、y2关于x的函数关系式?(3)、如果共有50人参加时,选择哪家旅行社合算?26. 某校办工厂有工人60名,生产某种由一个螺栓套两个螺母的配套产品,每人每天平均生产螺栓14个或螺母20个,应分配多少人生产螺栓,多少人生产螺母,能使生产出的螺栓和螺母刚好配套?27. 为了解我市的空气质量情况,某环保兴趣小组从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
请你根据图中提供的信息,解答下列问题:
(1)、请补全条形统计图,并求扇形统计图中表示“重度污染”的扇形的圆心角度数;(2)、所抽取若干天的空气质量情况的众数是中位数是 .(3)、请估计该市这一年(365天)达到“优”和“良”的总天数.28. 如图,在平面直角坐标系xOy中,矩形ABCD的边AD=3,A( ,0),B(2,0),直线y=kx+b经过B,D两点. (1)、求直线y=kx+b的解析式;(2)、将直线y=kx+b平移,若它与矩形有公共点,直接写出b的取值范围.
(1)、求直线y=kx+b的解析式;(2)、将直线y=kx+b平移,若它与矩形有公共点,直接写出b的取值范围.