华师大版数学九年级上册第24章解直角三角形24.2直角三角形的性质 同步练习
试卷更新日期：2015-11-12 类型：同步测试
一、选择题
-
1.
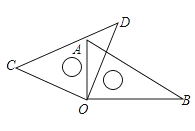
将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（ ）
A、140° B、160° C、170° D、150°2. Rt△ABC中，∠C=90°，∠B=46°，则∠A=（ ）A、44° B、34° C、54° D、64°3. 若一个三角形的三条高线交点恰好是此三角形的一个顶点，则此三角形一定是（ ）A、等腰三角形 B、等边三角形 C、等腰直角三角形 D、直角三角形4. 在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是（ ）A、120° B、90° C、60° D、30°5. 直角三角形的一个锐角是23°，则另一个锐角等于（ ）A、23° B、63° C、67° D、77°6. 在直角三角形中，其中一个锐角是另一个锐角的2倍，则此三角形中最小的角是（ ）A、15° B、30° C、60° D、90°7. 满足下列条件的△ABC ， 不是直角三角形的是（ ）A、∠C=∠A+∠B B、a：b：c=3：4：5 C、∠C=∠A-∠B D、∠A：∠B：∠C=3：4：58. 在直角三角形中，两个锐角的度数比为2：3，则较小锐角的度数为（ ）A、20° B、32° C、36° D、72°9. 已知△ABC是直角三角形，且∠C=90°，若∠A=34°，则∠B=（ ）A、66° B、56° C、46° D、146°10. 若直角三角形中的两个锐角之差为16°，则较大的一个锐角的度数是（ ）A、37° B、53° C、26° D、63°11. 如果直角三角形的一个锐角是另一个锐角的4倍，那么这个直角三角形中一个锐角的度数是（ ）A、9° B、18° C、27° D、36°12. △ABC中，∠C=90°，∠A：∠B=2：3，则∠A的度数为（ ）A、18° B、36° C、54° D、72°13. 若直角三角形中的两个锐角之差为22°，则较小的一个锐角的度数是（ ）A、24° B、34° C、44° D、46°14. Rt△ABC中，∠A=90°，角平分线AE、中线AD、高线AH的大小关系是（ ）A、AH＜AE＜AD B、AH＜AD＜AE C、AH≤AD≤AE D、AH≤AE≤AD15. 直角三角形两锐角的平分线相交得到的钝角为（ ）A、150o B、135o C、120o D、120o或135o二、填空题
-
16.
如图所示的三角板中的两个锐角的和等于 度．
17. Rt△ABC中，∠C=90°，∠A=35°30′，则∠B=.18.如图所示，在△ABC中，∠C=90°，EF∥AB ， ∠1=50°，则∠B的度数是度.
19.如图所示，BD⊥AC于点D ， DE∥AB ， EF⊥AC于点F ， 若BD平分∠ABC ， 则与∠CEF相等的角（不包括∠CEF）的个数是.
20. 已知Rt△ABC的两直角边长分别为3cm ， 4cm ， 斜边长为5cm ， 则斜边上的高等于cm.三、综合题
-
21.
如图，在直角三角形ABC中，∠ACB=90°，D是AB上一点，且∠ACD=∠B.
求证：CD⊥AB.
22. 在直角三角形中，有一个锐角是另一个锐角的4倍，求这个直角三角形各个角的度数.
