华师大版数学九年级上册第23章图形的相似23.4中位线 同步练习
试卷更新日期：2015-11-12 类型：同步测试
一、选择题
-
1. 如图，在△ABC中，点D、E分别是边AB，BC的中点．若△DBE的周长是6，则△ABC的周长是（ ）
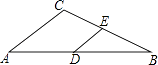A、8 B、10 C、12 D、142. 如图所示，A ， B两点分别位于一个池塘的两端，小聪想用绳子测量A ， B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A ， B的点C ， 找到AC ， BC的中点D ， E ， 并且测出DE的长为10m，则A ， B间的距离为（ ）
A、15m B、25m C、30m D、20m3.如图，△ABC中，AB=AC，AD平分∠BAC，DE∥AC交AB于E，则S△EBD：S△ABC=（ ）
A、1：2 B、1：4 C、1：3 D、2：34. 如果△ABC的两边长分别为3和5，那么连结△ABC三边中点D、E、F所得的△DEF的周长可能是（ ）A、3 B、4 C、5 D、65. 顺次连接四边形各边中点所得的四边形是（ ）A、平行四边形 B、矩形 C、菱形 D、以上都不对6. 平行四边形ABCD中，对角线AC、BD交于点O ， 点E是BC的中点 ． 若OE=3cm ， 则AB的长为（ ）A、3cm B、6cm C、9cm D、12cm7.如图所示，在梯形ABCD中，AB∥DC，EF是梯形的中位线，AC交EF于G，BD交EF于H，以下说法错误的是（ ）
A、AB∥EF B、AB+DC=2EF C、四边形AEFB和四边形ABCD相似 D、EG=FH8. 如图四边形ABCD ， AD∥BC ， AB⊥BC ， AD=1，AB=2，BC=3，P为AB边上的一动点，以PD ， PC为边作平行四边形PCQD ， 则对角线PQ的长的最小值是（ ）
A、3 B、4 C、5 D、69. 如图，梯形ABCD中，AD∥BC ， E、F分别是AB、CD的中点，EF分别交BD、AC于G、H ， 若AD=6，BC=10，则GH的长为（ ）
A、5 B、4 C、3 D、210. 如图，梯形ABCD中，∠ABC和∠DCB的平分线相交于梯形中位线EF上的一点P ， 若EF=2，则梯形ABCD的周长为（ ）
A、12 B、10 C、8 D、611. 如图所示，在平行四边形ABCD中，BC=4cm ， E为AD的中点，F、G分别为BE、CD的中点，则FG=（ ）cm ．
A、2 B、3 C、4 D、512.如图，在梯形ABCD中，AD∥BC ， E、F分别是AB、CD的中点，则下列结论：
①EF∥AD；②S△ABO=S△DCO；③△OGH是等腰三角形；④BG=DG；⑤EG=HF ．
其中正确的个数是（ ）
A、1个 B、2个 C、3个 D、4个13. 如图，梯形ABCD中，AD∥BC ， ∠B=30°，∠C=60°，E、F、M、N分别为AB、CD、BC、DA的中点，若BC=7，MN=3，则EF为（ ）
A、3 B、4 C、5 D、614. 已知：在等腰梯形ABCD中，AD∥BC ， AB=CD=4，MN是梯形ABCD的中位线，且MN=6，则梯形ABCD的周长是（ ）
A、22 B、20 C、18 D、1415. 梯形ABCD中AD∥BC ， E是AB的中点，过E作两底的平行线交DC于F ， 则下面结论错误的是（ ）A、EF平分线段AC B、梯形上下底间任意两点的连线段被EF平分 C、梯形EBCF与梯形AEFD周长之差的绝对值等于梯形两底之差的绝对值 D、梯形EBCF的面积比梯形AEFD的面积大二、填空题
-
16.
如图，在△ABC中，D、E分别是AB、AC的中点，若BC=10，则DE= ．
17.如图，点D、E、F分别是△ABC各边的中点，连接DE、EF、DF ． 若△ABC的周长为10，则△DEF的周长为 ．
18. 已知梯形的上底长为a ， 中位线长为m ， 那么这个梯形的下底长为.19.如图，在梯形ABCD中，AD∥BC ， 中位线EF交BD于点O ， 若FO-EO=6，则BC-AD为.
20.如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F ， AB=5，AC=2，则DF的长为.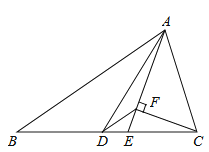
三、综合题
-
21.
如图，在△ABC中，AB=4，AC=3，AD、AE分别是△ABC角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，求线段EF的长．
22.如图，在△ABC中，若∠B=2∠C，AD⊥BC，E为BC边中点，求证：AB=2DE．
23. 请回答下列问题：(1)、叙述三角形中位线定理，并运用平行四边形的知识证明；
(2)、运用三角形中位线的知识解决如下问题：如图，在四边形ABCD中，AD∥BC ， E、F分别是AB ， CD的中点，求证：EF= （AD+BC）
