浙江省浙南名校联盟2018-2019学年高二上学期数学期末联考试卷
试卷更新日期:2019-04-02 类型:期末考试
一、单选题
-
1. 设集合 , ,则使 成立的 的值是( )A、-1 B、0 C、1 D、-1或12. 已知复数 ,则 ( )A、 B、 C、 D、3. 若 为实数,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 若变量 , 满足约束条件 ,则 的最大值是A、 B、 C、0 D、5. 在 中, 是 的中点, ,点 在 上且满足 ,则 等于( )
A、 B、 C、 D、6. 设函数 ,将 的图象向右平移 个单位后,所得的函数为偶函数,则 的值可以是A、1 B、 C、2 D、7. 函数 的图像可能是( )A、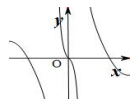 B、
B、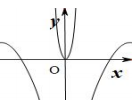 C、
C、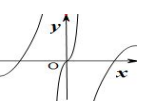 D、
D、 8. 设等差数列 的前 项和为 ,数列 的前 项和为 ,下列说法错误的是( )A、若 有最大值,则 也有最大值 B、若 有最大值,则 也有最大值 C、若数列 不单调,则数列 也不单调 D、若数列 不单调,则数列 也不单调9. 已知椭圆 和双曲线 有共同的焦点 , ,点 是 , 的交点,若 是锐角三角形,则椭圆 离心率 的取值范围是( )A、 B、 C、 D、10. 如图,在边长为1正方形 中,点 , 分别为边 , 的中点,将 沿 所在的直线进行翻折,将 沿 所在直线进行翻折,在翻折的过程中,下列说法错误的是( )
8. 设等差数列 的前 项和为 ,数列 的前 项和为 ,下列说法错误的是( )A、若 有最大值,则 也有最大值 B、若 有最大值,则 也有最大值 C、若数列 不单调,则数列 也不单调 D、若数列 不单调,则数列 也不单调9. 已知椭圆 和双曲线 有共同的焦点 , ,点 是 , 的交点,若 是锐角三角形,则椭圆 离心率 的取值范围是( )A、 B、 C、 D、10. 如图,在边长为1正方形 中,点 , 分别为边 , 的中点,将 沿 所在的直线进行翻折,将 沿 所在直线进行翻折,在翻折的过程中,下列说法错误的是( ) A、无论旋转到什么位置, 、 两点都不可能重合 B、存在某个位置,使得直线 与直线 所成的角为 C、存在某个位置,使得直线 与直线 所成的角为 D、存在某个位置,使得直线 与直线 所成的角为
A、无论旋转到什么位置, 、 两点都不可能重合 B、存在某个位置,使得直线 与直线 所成的角为 C、存在某个位置,使得直线 与直线 所成的角为 D、存在某个位置,使得直线 与直线 所成的角为二、填空题
-
11. 双曲线 的渐近线方程是;焦点坐标.12. 在 中,内角 , , 所对的边分别为 , , ,若 , ,则 ; 的面积是13. 已知某几何体的三视图如图所示,则该几何体的体积为;表面积为 .
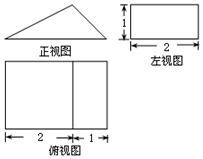 14. 若实数 , 满足 ,则 的最小值为.15. 已知直线 ,曲线 ,若直线 与曲线 相交于 、 两点,则 的取值范围是; 的最小值是.16. 点 是边长为2的正方形 的内部一点, ,若 ,则 的取值范围为.17. 函数 ,若此函数图象上存在关于原点对称的点,则实数 的取值范围是.18. 如图,在四棱锥 中, 平面 , , , , , .
14. 若实数 , 满足 ,则 的最小值为.15. 已知直线 ,曲线 ,若直线 与曲线 相交于 、 两点,则 的取值范围是; 的最小值是.16. 点 是边长为2的正方形 的内部一点, ,若 ,则 的取值范围为.17. 函数 ,若此函数图象上存在关于原点对称的点,则实数 的取值范围是.18. 如图,在四棱锥 中, 平面 , , , , , .
(Ⅰ)求证 平面 ;
(Ⅱ)求直线 与平面 所成线面角的正弦值.
三、解答题