浙江省金华市普通高中2018-2019学年高一上学期期末考试数学试题
试卷更新日期:2019-04-02 类型:期末考试
一、单选题
-
1. 已知集合 1,2, , ,则 的元素个数为A、2 B、3 C、4 D、82. 下列函数中,在区间 上为增函数的是( )A、 B、 C、 D、3. 平面向量 , 满足 ,如果 ,那么 等于A、 B、 C、 D、4. 最小正周期为 ,且图象关于直线 对称的一个函数是(A、 B、 C、 D、5. 已知 , , ,则x , y , z的大小关系是A、 B、 C、 D、6. 若 中,两个零点 , ,且 ,则A、 , B、 , C、 , D、 ,7. 函数 是偶函数,且函数 的图象关于点 成中心对称,当 时, ,则A、 B、 C、0 D、28. 函数 的图象是图中的A、
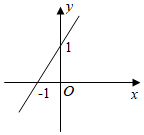 B、
B、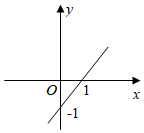 C、
C、 D、
D、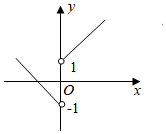 9. 已知向量 , 满足 , ,若 与 的夹角为 ,则m的值为A、2 B、 C、1 D、10. 已知函数 ,角A , B , C为锐角 的三个内角,则A、当 , 时, B、当 , 时, C、当 , 时, D、当 , 时,
9. 已知向量 , 满足 , ,若 与 的夹角为 ,则m的值为A、2 B、 C、1 D、10. 已知函数 ,角A , B , C为锐角 的三个内角,则A、当 , 时, B、当 , 时, C、当 , 时, D、当 , 时,二、填空题
-
11. 计算: ; .12. 函数 的定义域为;单调递减区间为 .13. 已知 ,则 ; .14. 已知两个向量 , ,
若 ,则 ;
若 , 的夹角为 ,则 .
15. 已知 是定义在R上的偶函数,且在区间 上单调递增,若实数a满足 ,则a的取值范围是 .16. 已知角 的顶点与原点重合,始边与x轴非负半轴重合,终边过点 ,则 .17. 已知二次函数 满足条件: ; ; 对任意实数x , 恒成立,则其解析式为 .三、解答题