广西钦州市2018-2019学年高二上学期文数期末考试试卷

试卷更新日期：2019-04-02 类型：期末考试

进入出卷网下载

一、单选题

1. 抛物线 $y^{2} = 16 x$ 的焦点坐标是（）

A、 $(- 4 ， 0)$ B、 $(4 ， 0)$ C、 $(0 ， - 4)$ D、 $(0 ， 4)$

查看试题解析
2. 某中学共有1000名学生，其中高一年级350人，该校为了了解本校学生视力情况，用分层抽样的方法从该校学生中抽出一个容量为100的样本进行调查，则应从高一年级抽取的人数为（）

A、20 B、25 C、30 D、35

查看试题解析
3. “三角形的三条边相等”是“三角形为等边三角形”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 抽查10件产品，设“至少抽到2件次品”为事件 $A$ ，则 $A$ 的对立事件是（）

A、至多抽到2件次品 B、至多抽到2件正品 C、至少抽到2件正品 D、至多抽到一件次品

查看试题解析
5. 如图是一个算法的程序框图，运行相应的程序，若输入 $x$ 的值为50，则输出的值是（）

A、30 B、40 C、50 D、60

查看试题解析
6. 已知命题 $p ： \forall x \in R$ ， $x^{2} + 2 > a$ ； $q ： \exists x \in R$ ， $x^{2} - 4 x + a \leq 0$ ，若“ $p$ 且 $q$ ”为真命题，则实数 $a$ 的取值范围是（）

A、 $(- \infty ， 2)$ B、 $(- \infty ， 4)$ C、 $(2 ， 4)$ D、 $[4 ， + \infty)$

查看试题解析
7. 若函数 $f (x) = x^{3} - 3 b x + 1$ 在区间 $(1 ， 2]$ 内是减函数， $b \in R$ ，则（）

A、 $b \leq 4$ B、 $b < 4$ C、 $b \geq 4$ D、 $b > 4$

查看试题解析
8. 曲线 $f (x) = 2 x - e^{x}$ 在点 $(0 ， f (0))$ 处的切线方程是（）

A、 $2 x - y - 1 = 0$ B、 $x - y + 1 = 0$ C、 $x - y = 0$ D、 $x - y - 1 = 0$

查看试题解析
9. 如图，圆 $C$ 内切于扇形 $A O B$ ， $∠ A O B = \frac{π}{3}$ ，若在扇形 $A O B$ 内任取一点，则该点不在圆 $C$ 内的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{3}{4}$

查看试题解析
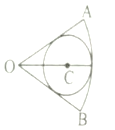10. 过抛物线 $x^{2} = y$ 的焦点 $F$ 的直线交抛物线于不同的两点 $A ， B$ ，则 $\frac{1}{| A F |} + \frac{1}{| B F |}$ 的值为（）

A、2 B、1 C、 $\frac{1}{4}$ D、4

查看试题解析
11. 已知椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ 的两个焦点是 $F_{1} ， F_{2}$ ，过点 $F_{2}$ 的直线交椭圆于 $A ， B$ 两点，在 $Δ A F_{1} B$ 中，若有两边之和是8，则第三边的长度为（）

A、3 B、4 C、5 D、6

查看试题解析
12. 某学校在数学联赛的成绩中抽取100名学生的笔试成绩，统计后得到如图所示的分布直方图，这100名学生成绩的中位数估值为（）

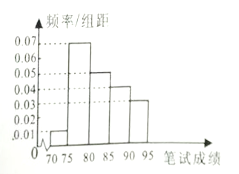A、80 B、82 C、82.5 D、84

查看试题解析
13. 秦久韶是我国南宋时期的著名数学家，他在其著作《数书九章》中提出的多项式求值的算法，被称为秦久韶算法，下图为用该算法对某多项式求值的程序框图，执行该程序框图，若输入的 $x = 2$ ，则输出的 $S$ 为（）

A、1 B、3 C、7 D、15

查看试题解析
14. 已知函数 $f (x)$ 是定义在 $R$ 上的偶函数，当 $x > 0$ 时， $x f^{'} (x) > f (x)$ ，若 $f (2) = 0$ ，则不等式 $\frac{f (x)}{x} > 0$ 的解集为（）

A、 ${x | - 2 < x < 0 或 0 < x < 2}$ B、 ${x | x 〈 - 2 或 x 〉 2}$ C、 ${x | - 2 < x 〈 0 或 x 〉 2}$ D、 ${x | x < - 2 或 0 < x < 2}$

查看试题解析
15. 若直线 $y = x + 1$ 与曲线 $y = x^{3} + b x^{2} + c$ 相切于点 $M (1 ， 2)$ ，则 $b + 2 c$ 等于（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

16. 若某中学高二年级8个班参加合唱比赛的得分如茎叶图所示，则这组数据的中位数是．

查看试题解析
17. 在某学校图书馆的书架上随意放着编号为1，2，3，4，5的五本书，若某同学从中任意选出2本书，则选出的2本书编号相连的概率为．

查看试题解析
18. 椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{m} = 1$ 的焦点坐标为 $(- 4 ， 0)$ 和 $(4 ， 0)$ ，则 $m$ 的值为．

查看试题解析
19. 期末考试结束后，某老师随机抽取了本班五位同学的数学成绩进行统计，五位同学平均每天学习数学的时间 $t$ （分钟）与数学成绩 $y$ 之间的一组数据如下表所示：

时间 $t$ （分钟）

30

40

70

90

120

数学成绩 $y$

35

48

$m$

82

92

通过分析，发现数学成绩 $y$ 与学习数学的时间 $t$ 具有线性相关关系，其回归方程为 $\hat{y} = 0.7 t + 15$ ，则表格中的 $m$ 的值是．

查看试题解析
20. 若回归直线 $\overset{\land}{y} = \overset{\land}{b} x + \overset{\land}{a}$ 的斜率估值为1.23，样本中心点为 $(4 ， 5)$ ，当 $x = 2$ 时，估计 $y$ 的值为．

查看试题解析

三、解答题

21. 已知 $m \in R$ ，命题 $p ：$ 方程 $\frac{x^{2}}{m - 1} + \frac{y^{2}}{2 - m} = 1$ 表示焦点在 $y$ 轴上的椭圆，命题 $q ：$ 方程 $\frac{x^{2}}{4 - m} - \frac{y^{2}}{m + 2} = 1$ 表示双曲线.

(1)、若命题 $p$ 是真命题，求实数 $m$ 的范围；

(2)、若命题“ $p$ 或 $q$ ”为真命题，“ $p$ 且 $q$ ”是假命题，求实数 $m$ 的范围.

查看试题解析
22. 读下列程序：
$I N P U T x$

$I F x < 0 T H E N$

$y = x^2$

$P R I N T y$

$E L S E$

$y = 2 * x$

$P R I N T y$

$E N D I F$

$E N D$

(1)、根据程序，画出对应的程序框图；

(2)、写出该程序表示的函数，并求出当输出的 $y = 4$ 时，输入的 $x$ 的值.

查看试题解析
23. 为了了解某城市居民用水量情况，我们抽取了100位居民某年的月均用水量（单位：吨）并对数据进行处理，得到该100位居民月均用水量的频率分布表，并绘制了频率分布直方图（部分数据隐藏）.

(1)、确定表中的 $x$ 与 $y$ 的值；

(2)、在上述频率分布直方图中，求从左往右数第4个矩形的高度；

(3)、在频率分布直方图中画出频率分布折线图.

查看试题解析
24. 将一颗质地均匀的骰子先后抛掷2次，观察向上的点数，并分别记为 $x ， y$ .

(1)、若记“ $x + y = 5$ ”为事件 $A$ ，求事件 $A$ 发生的概率；

(2)、若记“ $x^{2} + y^{2} \leq 10$ ”为事件 $B$ ，求事件 $B$ 发生的概率.

查看试题解析
25. 已知函数 $f (x) = a x^{3} + b x + c$ 为奇函数，曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线与直线 $x - 6 y - 7 = 0$ 垂直，导函数 $f' (x)$ 的最小值为-12.

(1)、求函数 $y = f (x)$ 的解析式；

(2)、用列表法求函数 $y = f (x)$ 在 $[- 1 ， 3]$ 上的单调增区间、极值、最值.

查看试题解析
26. 设抛物线 $C ： y^{2} = 2 x$ ，点 $A (2 ， 0)$ ， $B (- 2 ， 0)$ ，过点 $A$ 的直线 $l$ 与 $C$ 交于 $M$ ， $N$ 两点．

(1)、当 $l$ 与 $x$ 轴垂直时，求直线 $B M$ 的方程；

(2)、证明： $∠ A B M = ∠ A B N$ ．

查看试题解析

时间 $t$ （分钟）	30	40	70	90	120
数学成绩 $y$	35	48	$m$	82	92