广西钦州市2018-2019学年高二上学期理数期末考试试卷
试卷更新日期:2019-04-02 类型:期末考试
一、单选题
-
1. 抛物线 的焦点坐标是( )A、 B、 C、 D、2. 2018年央视大型文化节目《经典咏流传》的热播,在全民中掀起了诵读诗词的热潮,节目组为热心广众给以奖励,要从2018名观众中抽取50名幸运观众,先用简单随机抽样从2018人中剔除18人,剩下的2000人再按系统抽样的方法抽取50人,则在2018人中,每个人被抽到的可能性( )A、 均不相等 B、不全相等 C、都相等,且为 D、都相等,且为3. 若 为实数,则“ ”是“ ”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件4. 抽查10件产品,设“至少抽到2件次品”为事件 ,则 的对立事件是( )A、至多抽到2件次品 B、至多抽到2件正品 C、至少抽到2件正品 D、至多抽到一件次品5. 在空间直角坐标系中,已知点 ,过点 作平面 的垂线 ,垂足为 ,则点 的坐标为( )A、 B、 C、 D、6. 已知命题 , ; , ,若“ 且 ”为真命题,则实数 的取值范围是( )A、 B、 C、 D、7. 正四面体 中,D是AB边的中点,P是线段AD上的动点,记SP与BC所成角为 ,SP与底面ABC所成角为 ,二面角 为 ,则下列正确的是
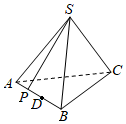 A、 B、 C、 D、8. 平面α的法向量为 =(1,2,-2),平面β的法向量 =(-2,h,k),若α∥β,则h+k的值为( )A、-2 B、-8 C、0 D、-69. 如图,圆 内切于扇形 , ,若在扇形 内任取一点,则该点不在圆 内的概率为( )
A、 B、 C、 D、8. 平面α的法向量为 =(1,2,-2),平面β的法向量 =(-2,h,k),若α∥β,则h+k的值为( )A、-2 B、-8 C、0 D、-69. 如图,圆 内切于扇形 , ,若在扇形 内任取一点,则该点不在圆 内的概率为( )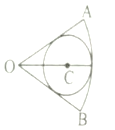 A、 B、 C、 D、10. 已知椭圆 的两个焦点分别为 ,点 在椭圆上, 是直角三角形,则 的面积为( )A、 B、 或4 C、 D、 或411. 设椭圆 的焦点与抛物线 的焦点相同,离心率为 ,则A、 B、 C、 D、12. 某学校在数学联赛的成绩中抽取100名学生的笔试成绩,统计后得到如图所示的分布直方图,这100名学生成绩的中位数估值为( )
A、 B、 C、 D、10. 已知椭圆 的两个焦点分别为 ,点 在椭圆上, 是直角三角形,则 的面积为( )A、 B、 或4 C、 D、 或411. 设椭圆 的焦点与抛物线 的焦点相同,离心率为 ,则A、 B、 C、 D、12. 某学校在数学联赛的成绩中抽取100名学生的笔试成绩,统计后得到如图所示的分布直方图,这100名学生成绩的中位数估值为( )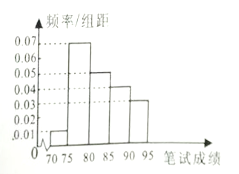 A、80 B、82 C、82.5 D、8413. 秦久韶是我国南宋时期的著名数学家,他在其著作《数书九章》中提出的多项式求值的算法,被称为秦久韶算法,下图为用该算法对某多项式求值的程序框图,执行该程序框图,若输入的 ,则输出的 为( )
A、80 B、82 C、82.5 D、8413. 秦久韶是我国南宋时期的著名数学家,他在其著作《数书九章》中提出的多项式求值的算法,被称为秦久韶算法,下图为用该算法对某多项式求值的程序框图,执行该程序框图,若输入的 ,则输出的 为( ) A、1 B、3 C、7 D、1514. 正方体 的棱长为1,则二面角 的余弦值为( )A、 B、 C、 D、15. 如图,正方体 的棱长为1,则点 到平面 的距离为( )
A、1 B、3 C、7 D、1514. 正方体 的棱长为1,则二面角 的余弦值为( )A、 B、 C、 D、15. 如图,正方体 的棱长为1,则点 到平面 的距离为( )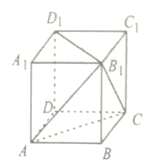 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
16. 若某中学高二年级8个班参加合唱比赛的得分如茎叶图所示,则这组数据的中位数是 .
 17. 某产品分为优质品、合格品、次品三个等级,生产中出现合格品的概率为0.25,出现次品的概率为0.03,在该产品中任抽一件,则抽到优质品的概率为 .18. 已知椭圆 ,直线 与椭圆 相交于 两点,点 是弦 的中点,则直线 的方程为 .19. 某公司调查了商品 的广告投入费用 (万元)与销售利润 (万元)的统计数据,如下表:
17. 某产品分为优质品、合格品、次品三个等级,生产中出现合格品的概率为0.25,出现次品的概率为0.03,在该产品中任抽一件,则抽到优质品的概率为 .18. 已知椭圆 ,直线 与椭圆 相交于 两点,点 是弦 的中点,则直线 的方程为 .19. 某公司调查了商品 的广告投入费用 (万元)与销售利润 (万元)的统计数据,如下表:广告费用 (万元)
2
3
5
6
销售利润 (万元)
5
7
9
11
由表中的数据得线性回归方程为 ,则当 时,销售利润 的估值为 .
其中: , .
20. 若回归直线 的斜率估值为1.23,样本中心点为 ,当 时,估计 的值为 .三、解答题
-
21. 已知 ,命题 方程 表示焦点在 轴上的椭圆,命题 方程 表示双曲线.(1)、若命题 是真命题,求实数 的范围;(2)、若命题“ 或 ”为真命题,“ 且 ”是假命题,求实数 的范围.22. 读下列程序:(1)、根据程序,画出对应的程序框图;(2)、写出该程序表示的函数,并求出当输出的 时,输入的 的值.23. 某高中三年级的甲、乙两个同学同时参加某大学的自主招生,在申请的材料中提交了某学科10次的考试成绩,记录如下:
甲:78 86 95 97 88 82 76 89 92 95
乙:73 83 69 82 93 86 79 75 84 99
(1)、根据两组数据,作出两人成绩的茎叶图,并通过茎叶图比较两人本学科成绩平均值的大小关系及方差的大小关系(不要求计算具体值,直接写出结论即可)(2)、现将两人的名次分为三个等级:成绩分数
等级
合格
良好
优秀
根据所给数据,从甲、乙获得“优秀”的成绩组合中随机选取一组,求选中甲同学成绩高于乙同学成绩的组合的概率.
24. 将一颗质地均匀的骰子先后抛掷2次,观察向上的点数,并分别记为 .(1)、若记“ ”为事件 ,求事件 发生的概率;(2)、若记“ ”为事件 ,求事件 发生的概率.