2018-2019学年初中数学湘教版九年级下册 第一章二次函数 单元卷

试卷更新日期：2019-04-02 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 下列函数是二次函数的是（  ）
    A、y=1x B、y=2x-3 C、y=3x2+1x2 D、y=8x2+1

    查看试题解析

  • 2. 已知二次函数y=（x+1）2+（x﹣3）2 ， 当函数y取最小值时，x的值是（   ）
    A、x=﹣1 B、x=3 C、x=2 D、x=1

    查看试题解析

  • 3. 二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：

    x

    …

    ﹣5

    ﹣4

    ﹣3

    ﹣2

    ﹣1

    0

    …

    y

    …

    4

    0

    ﹣2

    ﹣2

    0

    4

    …

    下列说法正确的是（   ）

    A、抛物线的开口向下 B、当x＞﹣3时，y随x的增大而增大 C、二次函数的最小值是﹣2 D、抛物线的对称轴是x= −52

    查看试题解析

  • 4. 下列抛物线中，与 轴有两个交点的是（     ）
    A、y=5x2-7x+5 B、y=16x2-24x+9 C、y=2x2+3x-4 D、y=3x2-2 6 x+2

    查看试题解析

  • 5. y=x2+（1-a）x+1是关于x的二次函数，当x的取值范围是1≤x≤3时，y在x=1时取得最大值，则实数a的取值范围是（　　）

    A、a=5 B、a≥5 C、a＝3 D、a≥3

    查看试题解析

  • 6. 将抛物线y=x2向右平移1个单位长度，再向上平移2个单位长度所得的抛物线解析式为（   ）
    A、y=（x﹣1）2+2 B、y=（x+1）2+2   C、y=（x﹣1）2﹣2 D、y=（x+1）2﹣2

    查看试题解析

  • 7. 二次函数y=ax2+bx+c（a≠0）的图象如图，以下结论正确的是（   ）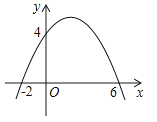

    A、abc＞0 B、方程ax2+bx+c=0有两个实数根分别为-2和6 C、a-b+c＜0 D、当y=4时，x的取值只能为0

    查看试题解析

  • 8. 把抛物线y=ax2+bx+c的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式为y=x2-2x+3，则b+c的值为（    ）

    A、9 B、12 C、-14 D、10

    查看试题解析

  • 9.

    已知二次函数y=ax2+bx+c的图象如图所示，记m=|a﹣b+c|+|2a+b+c|，n=|a+b+c|+|2a﹣b﹣c|．则下列选项正确的是（　　）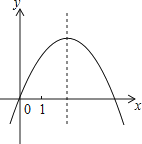

    A、m＜n B、m＞n C、m=n D、m、n的大小关系不能确定

    查看试题解析

二、填空题

  • 10. 二次函数 y=2(x+1)2−3 的顶点坐标是 ．

    查看试题解析

  • 11. 已知函数 y＝(m＋2) xm2−2 是二次函数，则m等于

    查看试题解析

  • 12. 将抛物线y=x2向左平移1个单位后的抛物线表达式为 ．

    查看试题解析

  • 13. 二次函数y=x2+4x+3与坐标轴交于A、B、C三点，则三角形ABC的面积为 ．

    查看试题解析

  • 14. 有一个角是60°的直角三角形，它的面积S与斜边长x之间的函数关系式是 ．

    查看试题解析

  • 15. 若二次函数y=x2﹣mx+1的图象与x轴有且只有一个公共点，则m= ．

    查看试题解析

  • 16. 抛物线y=x2﹣5x+6与x轴的交点坐标是 ．

    查看试题解析

  • 17. 将y=2x2﹣12x﹣12变为y=a（x﹣m）2+n的形式，则m•n= ．

    查看试题解析

  • 18. 如图，边长为1的正方形ABCO，以A为顶点，且经过点C的抛物线与对角线交于点D，点D的坐标为 ．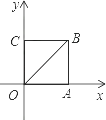

    查看试题解析

  • 19. 如图，把抛物线y= 12 x2平移得到抛物线m，抛物线m经过点A（﹣6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y= 12 x2交于点Q，则图中阴影部分的面积为 ．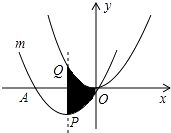

    查看试题解析

三、解答题

  • 20. 如图，用50m长的护栏全部用于建造一块靠墙的长方形花园，写出长方形花园的面积y（m2）与它与墙平行的边的长x（m）之间的函数．

    查看试题解析

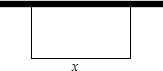  • 21. 某商场销售某种品牌的手机，每部进货价为2500元.市场调研表明：当销售价为2900元时，平均每天能售出8部；而当销售价每降低50元时，平均每天就能多售出4部.
    (1)、当售价为2800元时，这种手机平均每天的销售利润达到多少元?
    (2)、若设每部手机降低x元，每天的销售利润为y元，试写出y与x之间的函数关系式．
    (3)、商场要想获得最大利润，每部手机的售价应订为为多少元？此时的最大利润是多少元？

    查看试题解析

  • 22. 如图，矩形ABCD的两边长AB=18cm，AD=4cm，点P、Q分别从A、B同时出发，P在边AB上沿AB方向以每秒2cm的速度匀速运动，Q在边BC上沿BC方向以每秒1cm的速度匀速运动．设运动时间为x秒，△PBQ的面积为y（cm2）.

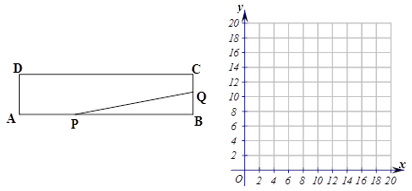    (1)、求y关于x的函数关系式，并在右图中画出函数的图象；
    (2)、求△PBQ面积的最大值.

    查看试题解析

  • 23. 如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）的图象经过M（1，0）和N（3，0）两点，且与y轴交于D（0，3），直线l是抛物线的对称轴．

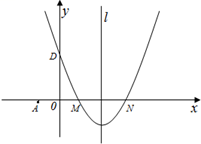    (1)、求该抛物线的解析式．
    (2)、若过点A（﹣1，0）的直线AB与抛物线的对称轴和x轴围成的三角形面积为6，求此直线的解析式．
    (3)、点P在抛物线的对称轴上，⊙P与直线AB和x轴都相切，求点P的坐标．

    查看试题解析

  • 24. 已知二次函数y=- 14x2+32x 的图象如图．

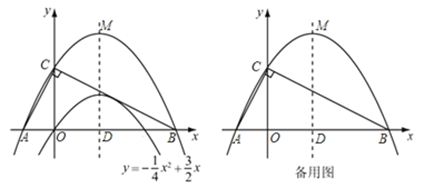    (1)、求它的对称轴与x轴交点D的坐标；
    (2)、将该抛物线沿它的对称轴向上平移，设平移后的抛物线与x轴，y轴的交点分别为A、B、C三点，若∠ACB=90°，求此时抛物线的解析式；
    (3)、设（2）中平移后的抛物线的顶点为M，以AB为直径，D为圆心作⊙D，试判断直线CM与⊙D的位置关系，并说明理由．

    查看试题解析

  • 25. 如图，梯形ABCD中，AB∥CD，AB=14，AD=4 2 ，CD=7．直线l经过A、D两点，且sin∠DAB= 22 ．动点P在线段AB上从点A出发以每秒2个单位的速度向点B运动，同时动点Q从点B出发以每秒5个单位的速度沿B→C→D的方向向点D运动，过点P作PM垂直于AB，与折线A→D→C相交于点M，当P，Q两点中有一点到达终点时，另一点也随之停止运动．设点P、Q运动的时间为t秒（t＞0），△MPQ的面积为S．

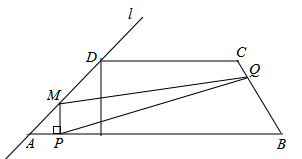    (1)、求腰BC的长；
    (2)、当Q在BC上运动时，求S与t的函数关系式；
    (3)、在（2）的条件下，是否存在某一时刻t，使得△MPQ的面积S是梯形ABCD面积的 14 ？若存在，请求出t的值；若不存在，请说明理由；
    (4)、随着P，Q两点的运动，当点M在线段DC上运动时，设PM的延长线与直线l相交于点N，试探究：当t为何值时，△QMN为等腰三角形？

    查看试题解析

  • 26. 已知直线l：y=kx和抛物线C：y=ax2+bx+1．

    （Ⅰ）当k=1，b=1时，抛物线C：y=ax2+bx+1的顶点在直线l：y=kx上，求a的值；

    （Ⅱ）若把直线l向上平移k2+1个单位长度得到直线r，则无论非零实数k取何值，直线r与抛物线C都只有一个交点；

    （i）求此抛物线的解析式；

    （ii）若P是此抛物线上任一点，过点P作PQ∥y轴且与直线y=2交于点Q，O为原点，求证：OP=PQ．

    查看试题解析

  • 27. 甲、乙两人进行羽毛球比赛，羽毛球飞行的路线为抛物线的一部分. 如图，甲 在O点正上方1m的P处发出一球，羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 y=a（x-4）2+h  ，已知点O与球网的水平距离为5m，球网的高度1.55m.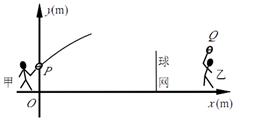

    (1)、当a=- 124 时，①求h的值；②通过计算判断此球能否过网.
    (2)、若甲发球过网后，羽毛球飞行到与点O的水平距离为7m，离地面的高度为 125  m的Q处时，乙扣球成功，求a的值.   

    查看试题解析