2018-2019学年初中数学湘教版九年级下册 第二章圆 单元卷
试卷更新日期：2019-04-02 类型：单元试卷
一、单选题
-
1. 如果一个扇形的半径是1，弧长是 ，那么此扇形的圆心角的大小为（ ）A、30° B、45° C、60° D、90°2. 将一个圆分割成三个扇形，它们的圆心角的度数之比为2：3：4，则这个扇形圆心角的度数为（ ）A、30°，60°，90° B、60°，120°，180° C、50°，100°，150° D、80°，120°，160°3. 已知扇形的圆心角为150°，半径为6cm，则该扇形的面积为（ ）A、5πcm2 B、15πcm2 C、20πcm2 D、30πcm24. 如图，△ABC是⊙O的内接三角形，若∠ABC=70°，则∠AOC的大小是（ ）
A、20° B、35° C、130° D、140°5. 如图，已知半径OD与弦AB互相垂直，垂足为点C，若AB=8cm，CD=3cm，则圆O的半径为（ ）
A、 cm B、5cm C、4cm D、 cm6. 下列说法中正确的是（ ）A、弦是直径 B、弧是半圆 C、半圆是圆中最长的弧 D、直径是圆中最长的弦7.如图，PA、PB分别是⊙O的切线，A、B为切点，AC是⊙O的直径，已知∠BAC=35°，∠P的度数为（ ）
A、35° B、45° C、60° D、70°8.如图，在Rt△ABC中，∠C=90°，∠B=60°，内切圆O与边AB、BC、CA分别相切于点D、E、F，则∠DEF为（ ）
A、55° B、60° C、75° D、80°9. 如图，AB是⊙O的直径，CD是弦，如果弧AC=弧AD，∠C比∠D大36°，则∠A等于（ ）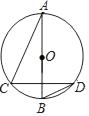
A、24° B、27° C、34° D、37°10. 如图，直线AB与⊙O相切于点A，⊙O的半径为2，若∠OBA = 30°，则OB的长为（ ）
A、 B、4 C、 D、2二、填空题
-
11. 已知，如图，半径为1的⊙M经过直角坐标系的原点O，且与x轴、y轴分别交于点A、B，点A的坐标为( ，0)，⊙M的切线OC与直线AB交于点C.则∠ACO＝.
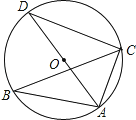
12.如图，△ABC内接于⊙O，AD是⊙O的直径，∠ABC=30°，则∠CAD=度．
13. 已知弦AB与CD交于点E，弧 的度数比弧 的度数大20°，若∠CEB=m°，则∠CAB=（用关于m的代数式表示）．14. 如图所示，AB为⊙O的直径，P点为其半圆上一点，∠POA=40°，C为另一半圆上任意一点（不含A、B），则∠PCB＝度．
15.如图，正△ABC的边长为2，以AB为直径作⊙O，交AC于点D， 交BC于点E，连接DE，则图中阴影部分的面积为；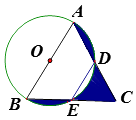
16. 如图，AB为⊙O的弦，半径OD⊥AB于点C．若AB=8，CD=2，则⊙O的半径长为 ．
17. 如图，若 = ，PAB、PCD是⊙O的两条割线，PAB过圆心O，∠P=30°，则∠BDC= ．
18. 如图矩形ABCD中，AB=1，AD= ，以AD的长为半径的⊙A交BC于点E，则图中阴影部分的面积为 ．
19. 如图，正方形ABCD内接于⊙O，其边长为4，则⊙O的内接正三角形EFG的边长为 ．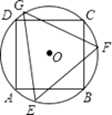
20. 如图，直线AB与半径为2的⊙O相切于点C，点D、E、F是⊙O上三个点，EF//AB，若EF=2 ，则 ∠EDC 的度数为.
三、解答题
-
21. 如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，若∠PAB=40°，求∠P的度数．
22. 如图，已知AB是⊙O的弦，C是的中点，AB=8，AC= ，求⊙O半径的长．
23. 如图，在⊙O中，AB=CD.求证：AD=BC.
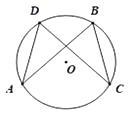24. 已知：如图，AB是⊙O的弦，半径OC、OD分别交AB于点E、F，且OE=OF．求证：AE=BF．
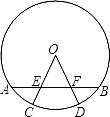25.如图，CB是⊙O的直径，P是CB延长线上一点，PB=2，PA切⊙O于A点，PA=4．求⊙O的半径．
26.如图，在⊙O中，过弦AB的中点E作弦CD，且CE=2，DE=4，求弦AB的长．
27. 如图为桥洞的形状，其正视图是由 和矩形ABCD构成．O点为 所在⊙O的圆心，点O又恰好在AB为水面处．若桥洞跨度CD为8米，拱高（OE⊥弦CD于点F）EF为2米．求 所在⊙O的半径DO．
28. 已知：如图，AB是圆O的直径，C是圆O上一点，CD⊥AB，垂足为点D，F是弧AC的中点，OF与AC相交于点E，AC=8 cm，EF=2cm.
(1)、求AO的长；(2)、求sinc的值.
