2018-2019学年初中数学人教版七年级下册 第五章相交线与平行线 单元卷(A)
试卷更新日期:2019-04-02 类型:单元试卷
一、选择题
-
1.
如图,已知a∥b,∠1=65°,则∠2的度数为( )
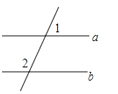 A、65° B、125° C、115° D、25°2. 下列命题:
A、65° B、125° C、115° D、25°2. 下列命题:①两条直线被第三条直线所截,同位角相等;
②两点之间,线段最短;
③相等的角是对顶角;
④同角或等角的补角相等。
其中是真命题的有( )个。
A、1 B、2 C、3 D、43. 将一直角三角板与两边平行的纸条如图放置.已知∠1=30°,则∠2的度数为( )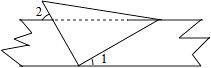 A、30° B、45° C、50° D、60°4. 如果线段AB与线段CD没有交点,则( )A、线段AB与线段CD一定平行 B、线段AB与线段CD一定不平行 C、线段AB与线段CD可能平行 D、以上说法都不正确5. 尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是( )A、
A、30° B、45° C、50° D、60°4. 如果线段AB与线段CD没有交点,则( )A、线段AB与线段CD一定平行 B、线段AB与线段CD一定不平行 C、线段AB与线段CD可能平行 D、以上说法都不正确5. 尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是( )A、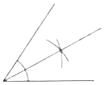 B、
B、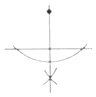 C、
C、 D、
D、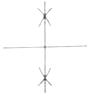 6. 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
6. 如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( ) A、60° B、50° C、40° D、30°7. 如图,已知直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数为( )
A、60° B、50° C、40° D、30°7. 如图,已知直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数为( )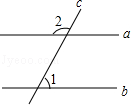 A、30° B、60° C、120° D、150°8. 下列说法中,正确的是( )A、在同一平面内,两条直线的位置关系只有相交,平行两种 B、在同一平面内,不相交的两条线段互相平行 C、在同一平面内,不相交的两条直线互相平行 D、在同一平面内,不相交的两条射线互相平行9.
A、30° B、60° C、120° D、150°8. 下列说法中,正确的是( )A、在同一平面内,两条直线的位置关系只有相交,平行两种 B、在同一平面内,不相交的两条线段互相平行 C、在同一平面内,不相交的两条直线互相平行 D、在同一平面内,不相交的两条射线互相平行9.如图,∠1=∠2,∠3=40°,则∠4等于( )
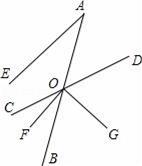
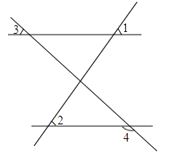 A、120° B、130° C、140° D、40°10. 如图直线AB、CD相交于点O,∠1=∠2,若∠AOE=140°,则∠AOC的度数为( )
A、120° B、130° C、140° D、40°10. 如图直线AB、CD相交于点O,∠1=∠2,若∠AOE=140°,则∠AOC的度数为( ) A、50° B、60° C、70° D、80°11. 挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走。如图中,按照这一规则,第1次应拿走⑨号棒,第2次应拿走⑤号棒,…,则第6次应拿走( )
A、50° B、60° C、70° D、80°11. 挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走。如图中,按照这一规则,第1次应拿走⑨号棒,第2次应拿走⑤号棒,…,则第6次应拿走( )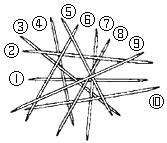
A、②号棒 B、⑦号棒 C、⑧号棒 D、⑩号棒12. 如图,直线l1∥l2 , ∠A=125°,∠B=85°,则∠1+∠2=( ) A、30° B、35° C、36° D、40°13. 已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )
A、30° B、35° C、36° D、40°13. 已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )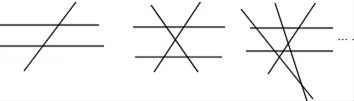 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题
-
14. 如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2=°
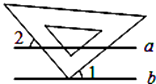
 15.
15.如图,已知 a ∥ b ,小亮把三角板的直角顶点放在直线 b 上.若∠1=40°,则∠2的度数为 .
 16. 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是 .
16. 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是 .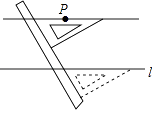 17. 两个角的两边两两互相平行,且一个角的 等于另一个角的 ,则这两个角的度数分别为度,度.18. 如图,直线 相交于点 于点 ,连接 .
17. 两个角的两边两两互相平行,且一个角的 等于另一个角的 ,则这两个角的度数分别为度,度.18. 如图,直线 相交于点 于点 ,连接 .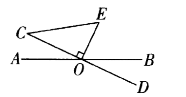 (1)、若 ,则 =;(2)、若 =2 cm, =1.5 cm, =2.5 cm,则点 到 的距离是cm.
(1)、若 ,则 =;(2)、若 =2 cm, =1.5 cm, =2.5 cm,则点 到 的距离是cm.三、解答题
-
19. 已知,如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
证明:∵AD∥BE(已知),
∴∠A=∠ ▲ ( ▲ )
又∵∠1=∠2(已知),
∴AC∥ ▲ ( ▲ ),
∴∠3=∠ ▲ ( ▲ ),
∴∠A=∠E(等量代换).
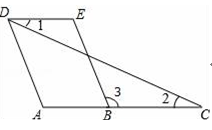 20. 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
20. 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数. 21. 如图,直线AB、CD相交于点O,若∠AOE=40°,OA平分∠COE,求∠BOD的度数.
21. 如图,直线AB、CD相交于点O,若∠AOE=40°,OA平分∠COE,求∠BOD的度数. 22.
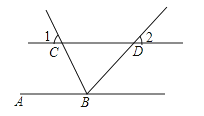
22.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
 23. 如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.
23. 如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.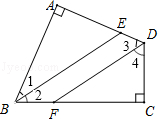 24. 如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°,求证AB∥CD
24. 如图,直线AB,CD,EF被直线GH所截,∠1=70°,∠2=110°,∠3=70°,求证AB∥CD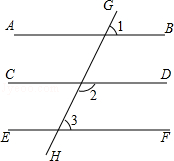
证明:∵∠1=70°,∠3=70°
∴∠3=∠1 ▲ .
∴ ▲ ∥ ▲ .
∵∠2=110°,∠3=70°(已知)
∴ ▲ + ▲ =180° (等式的性质)
∴ ▲ ∥ ▲ .
∴AB∥CD ▲ .