2018-2019学年初中数学人教版七年级下册第六章实数单元卷（B）

试卷更新日期：2019-04-02 类型：单元试卷

进入出卷网下载

一、选择题

1. 4的平方根是（）

A、±2 B、2 C、 $\pm \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 下列各式化简后，结果为无理数的是（）

A、 $\sqrt{{(- 8)}^{2}}$ B、 $\sqrt[3]{64}$ C、 $\sqrt{9}$ D、 $\sqrt{12}$

查看试题解析
3. 如图，已知数轴上的点A、B、C、D分别表示数-2、1、2、3，则表示3－ $\sqrt{5}$ 的点P应落在线段（）

A、AO上 B、OB上 C、BC上 D、CD上

查看试题解析
4. 下列等式成立的是（）

A、 $\sqrt[3]{3}$ =1 B、 $\sqrt[3]{\frac{1}{6}}$ = $\frac{1}{2}$ C、 $\sqrt[3]{- 9}$ =﹣3 D、 $\sqrt[3]{- 27}$ =﹣3

查看试题解析
5. 估计 $\sqrt{65}$ 的值在（）

A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间

查看试题解析
6. 已知实数x，y满足 $\sqrt{x - 2} + {(y + 1)}^{2} = 0$ ，则x﹣y等于（）

A、3 B、﹣3 C、1 D、﹣1

查看试题解析
7. 若实数a，b在数轴上的位置如图所示，则以下说法正确的是（）

A、a＞b B、ab＞0 C、a+b＞0 D、|a|＞|b|

查看试题解析
8. 实数 $\sqrt{a^{2}}$ 的平方根为（）

A、a B、±a C、± $\sqrt{a}$ D、 $\pm \sqrt{| a |}$

查看试题解析
9. 如图，数轴上的A、B、C、D四点中，与数﹣ $\sqrt{3}$ 表示的点最接近的是（）

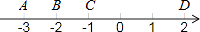A、点A B、点B C、点C D、点D

查看试题解析
10. 若实数a、b、c在数轴上对应点的位置如图所示，则下列不等式成立的是（）

A、ac>bc B、ab>cb C、a+c>b+c D、a+b>c+b

查看试题解析
11. 对于实数a，b，c，d，规定一种运算 $| \begin{matrix} a & b \\ c & d \end{matrix} |$ =ad﹣bc，如 $| \begin{matrix} 1 & 0 \\ 2 & (- 2) \end{matrix} |$ =1×（﹣2）﹣0×2=﹣2，那么当 $| \begin{matrix} 2 x & x \\ - x & x \end{matrix} |$ =6时，x的值为（）

A、 $\sqrt{6}$ B、± $\sqrt{6}$ C、 $\sqrt{2}$ D、± $\sqrt{2}$

查看试题解析

二、填空题

12. 化简： $\sqrt{{(- 3)}^{2}}$ = ．

查看试题解析
13. 已知2b+1的平方根为±3，3a+2b﹣1的算术平方根为4，则2b﹣3a的立方根是．

查看试题解析
14. 设n为正整数，且n＜ $\sqrt{65}$ ＜n+1，则n的值为．

查看试题解析
15. 若关于x的方程﹣2x+m $\sqrt{2017 - x}$ +4020=0存在整数解，则正整数m的所有取值的和为．

查看试题解析
16. 设a、b、c都是实数，且满足 ${(2 - a)}^{2} + \sqrt{a^{2} + b + c} + | c + 8 | = 0$ ，ax²+bx+c=0；则代数式x²+2x+1的值为．

查看试题解析
17. 实数a，n，m，b满足a＜n＜m＜b，这四个数在数轴上对应的点分别为A，N，M，B（如图），若AM²=BM•AB，BN²=AN•AB，则称m为a，b的“大黄金数”，n为a，b的“小黄金数”，当b﹣a=2时，a，b的大黄金数与小黄金数之差m﹣n= ．

查看试题解析

三、解答题

18. 利用平方根、立方根来解下列方程．

(1)、x²﹣169=0；

(2)、（2x﹣1）²﹣1=0；

(3)、 $\frac{27}{4}$ x³﹣2=0；

(4)、 $\frac{1}{2}$ （x+3）³=4．

查看试题解析
19. 已知2a﹣1的平方根是±3，3a+b﹣9的立方根是2，c是 $\pm \sqrt{57}$ 的整数部分，求a+2b+c的算术平方根．

查看试题解析
20. 已知m是 $\sqrt{13}$ 的整数部分，n是 $\sqrt{13}$ 的小数部分，求 $\frac{m - n}{m + n}$ 的值．

查看试题解析
21.

(1)、一个正数的平方根是a+3与2a﹣15，求a的值．

(2)、已知 $\sqrt{a - 16} + {(b + 2)}^{2} = 0$ ，求 $\frac{a}{b}$ 的立方根．

(3)、已知x、y为实数，且 $y = \sqrt{x - 9} - \sqrt{9 - x} + \sqrt{4}$ ．求 $\sqrt{x} + \sqrt{y}$ 的值．

查看试题解析
22. 某地开辟了一块长方形的荒地，新建一个以环保为主题的公园，已知这块荒地的长是宽的2倍，它的面积为400000平方米．

(1)、公园的宽大约是多少？它有1000米吗？

(2)、如果要求误差小于10米，它的宽大约是多少米？

查看试题解析
23. 阅读下面的文字，解答问题
大家知道， $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $\sqrt{2}$ ﹣1来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？

事实上，小明的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．

又例如因为 $\sqrt{4}$ ＜ $\sqrt{7}$ ＜ $\sqrt{9}$ ，即2＜ $\sqrt{7}$ ＜3，所以行的整数部分为2，小数部分为 $\sqrt{7}$ ﹣2．

请解答

(1)、 $\sqrt{83}$ 的整数部分为；小数部分为；

(2)、有人说，如果 $\sqrt{83}$ 的整数部分为x， $\sqrt{97}$ 的小数部分记为y，则x+y= $\sqrt{97}$ ，你认为对吗？为什么？

(3)、如果 $\sqrt{35}$ 的整数部分为a， $\sqrt{35}$ 的小数部分为b，求a﹣2b+2 $\sqrt{35}$ 的值．

查看试题解析
24. 如图，在一张长方形纸条上画一条数轴．

(1)、若折叠纸条，数轴上表示﹣3的点与表示1的点重合，则折痕与数轴的交点表示的数为；

(2)、若经过某次折叠后，该数轴上的两个数a和b表示的点恰好重合，则折痕与数轴的交点表示的数为（用含a，b的代数式表示）；

(3)、若将此纸条沿虚线处剪开，将中间的一段纸条对折，使其左右两端重合，这样连续对折n次后，再将其展开，请分别求出最左端的折痕和最右端的折痕与数轴的交点表示的数．（用含n的代数式表示）

查看试题解析
25. 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．小白在草稿纸上画了一条数轴进行操作探究：

(1)、操作一：
折叠纸面，若使表示的点1与﹣1表示的点重合，则﹣2表示的点与表示的点重合；

(2)、操作二：
折叠纸面，若使1表示的点与﹣3表示的点重合，回答以下问题：

① $\sqrt{3}$ 表示的点与数表示的点重合；

②若数轴上A．B两点之间距离为8（A在B的左侧），且A．B两点经折叠后重合，则A．B两点表示的数分别是；

(3)、操作三：
在数轴上剪下9个单位长度（从﹣1到8）的一条线段，并把这条线段沿某点折叠，然后在重叠部分某处剪一刀得到三条线段（如图）．若这三条线段的长度之比为1：1：2，则折痕处对应的点所表示的数可能是．

查看试题解析

2018-2019学年初中数学人教版七年级下册 第六章实数 单元卷（B）

一、选择题

二、填空题

三、解答题

2018-2019学年初中数学人教版七年级下册第六章实数单元卷（B）