2018-2019学年初中数学人教版七年级下册第六章实数单元卷（A）

试卷更新日期：2019-04-02 类型：单元试卷

进入出卷网下载

一、选择题

1. $- \sqrt{5}$ 的绝对值是（）

A、 $- \frac{1}{\sqrt{5}}$ B、 $- \sqrt{5}$ C、 $\sqrt{5}$ D、5

查看试题解析
2. 4的平方根是；4的算术平方根是

查看试题解析
3. 已知m= $\sqrt{4}$ + $\sqrt{3}$ ，则以下对m的估算正确的（）

A、2＜m＜3 B、3＜m＜4 C、4＜m＜5 D、5＜m＜6

查看试题解析
4. 估计 $\sqrt{7}$ +1的值（）

A、在1和2之间 B、在2和3之间 C、在3和4之间 D、在4和5之间

查看试题解析
5. 实数a，b在数轴上的对应点的位置如图所示，把﹣a，﹣b，0按照从小到大的顺序排列，正确的是（）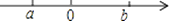

A、﹣a＜0＜﹣b B、0＜﹣a＜﹣b C、﹣b＜0＜﹣a D、0＜﹣b＜﹣a

查看试题解析
6. 在实数：0， $\sqrt{2}$ ， $- \frac{1}{3}$ ，0.74，π中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 点A，B在数轴上的位置如图所示，其对应的实数分别是a，b，下列结论错误的是（）

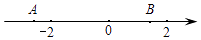A、|b|＜2＜|a| B、1﹣2a＞1﹣2b C、﹣a＜b＜2 D、a＜﹣2＜﹣b

查看试题解析
8. 实数 $\sqrt{a^{2}}$ 的平方根为（）

A、a B、±a C、± $\sqrt{a}$ D、± $\sqrt{| a |}$

查看试题解析
9. 下列四个命题，正确的有（）个．
①有理数与无理数之和是有理数；②有理数与无理数之和是无理数；③无理数与无理数之和是无理数；④无理数与无理数之积是无理数．

A、1 B、2 C、3 D、4

查看试题解析
10. 若方程（x﹣5）²=19的两根为a和b，且a＞b，则下列结论中正确的是（）

A、a是19的算术平方根 B、b是19的平方根 C、a﹣5是19的算术平方根 D、b+5是19的平方根

查看试题解析
11. 若a $< \sqrt{7} - 2 < b$ ，且a、b是两个连续整数，则a+b的值是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

12. 在实数π， $\sqrt{2} - 1$ ， $\sqrt[3]{8}$ ， $\frac{3}{7}$ ，- $\sqrt[3]{9}$ ，0.2121121112…（每两个2之间依次多一个1）中，无理数共有个．

查看试题解析
13. 若a＜ $\sqrt{30}$ ＜b，且a，b是两个连续的整数，则a+b的值为．

查看试题解析
14. 化简： $| \sqrt{3} - 2 |$ = ．

查看试题解析
15. 用适当的符号填空：若b＞c＞0，则b﹣c0，|c﹣b|0， $\sqrt{c}$ ﹣ $\sqrt{b}$ 0．

查看试题解析
16. 一般地，我们把研究对象统称为元素，把一些元素组成的总体称为集合．一个给定集合中的元素是互不相同的，也就是说，集合中的元素是不重复出现的．如一组数1，1，2，3，4就可以构成一个集合，记为A={1，2，3，4}．类比实数有加法运算，集合也可以“相加”．定义：集合A与集合B中的所有元素组成的集合称为集合A与集合B的和，记为A+B．若A={﹣2，0，1，5，7}，B={﹣3，0，1，3，5}，则A+B= ．

查看试题解析
17. 将1、 $\sqrt{2}$ 、 $\sqrt{3}$ 、 $\sqrt{6}$ 按右侧方式排列．若规定（m，n）表示第m排从左向右第n个数，则（7，3）所表示的数是；（5，2）与（20，17）表示的两数之积是．

查看试题解析

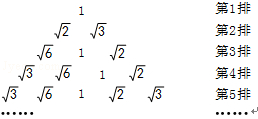
三、解答题

18. 判断下面说法是否正确，并举例说明理由．

(1)、两个无理数的和一定是无理数；

(2)、两个无理数的积一定是无理数．

查看试题解析
19. 计算： $\sqrt[3]{8}$ ﹣ $\sqrt{\frac{4}{25}}$ ．

查看试题解析
20. 把下列各数分别填在相应的集合中：﹣ $\frac{11}{12}$ ， $\sqrt[3]{2}$ ，﹣ $\sqrt{4}$ ，0，﹣ $\sqrt{0.4}$ ， $\sqrt[3]{8}$ 、 $\frac{π}{4}$ ， $0. \dot{2} \dot{3}$ ，3.14

查看试题解析
21.

(1)、计算： $\sqrt[3]{- 0.125}$ +| $\sqrt{3}$ ﹣2|﹣ $\sqrt{3 - \frac{3}{4}}$ + $\sqrt{3}$ ﹣ $\sqrt{{(- 2)}^{2}}$

(2)、一个正数的平方根是2x+4和﹣3x﹣2，求这个数的立方根．

查看试题解析
22. 已知M= $\sqrt[2 m + n - 3]{m + 3}$ 是m+3的算术平方根，N= $\sqrt[2 m - n]{n - 2}$ 是n﹣2的立方根．求（n﹣m）²⁰⁰⁸ ．

查看试题解析
23. 已知x﹣2的一个平方根是﹣2，2x+y﹣1的立方根是3，求x+y的算术平方根．

查看试题解析
24. 求值：

(1)、已知（x﹣1）²=4，求x的值；

(2)、 $\sqrt{2} (\sqrt{2} + 2) + | \sqrt{2} - \sqrt{3} |$

查看试题解析
25. 讲解完本节，王老师在小结时总结了这样一句话：“对于任意两个整数a、b，如果a＞b，那么 $\sqrt{a}$ ＞ $\sqrt{b}$ ．”然后讲了下面的一个例题：比较 $\frac{1}{5} \sqrt{200}$ 和 $2 \sqrt{3}$ 的大小．
方法一： $\frac{1}{5} \sqrt{200}$ = $\sqrt{\frac{1}{25} \times 200}$ = $\sqrt{8}$ ， $2 \sqrt{3}$ = $\sqrt{4 \times 3}$ = $\sqrt{12}$ ，

又∵8＜12，

∴ $\frac{1}{5} \sqrt{200}$ ＜ $2 \sqrt{3}$ ．

方法二： ${(\frac{1}{5} \sqrt{200})}^{2}$ = $\frac{1}{25}$ ×200=8， ${(2 \sqrt{3})}^{2}$ =4×3=12．

又∵8＜12，

∴ $\frac{1}{5} \sqrt{200}$ ＜ $2 \sqrt{3}$ ．

根据上面的例题解答下列各题：

(1)、比较 $- 5 \sqrt{6}$ 和 $- 6 \sqrt{5}$ 的大小；

(2)、比较 $\sqrt{7}$ ﹣1与 $\sqrt{5}$ ﹣ $\sqrt{3}$ 的大小．

查看试题解析

2018-2019学年初中数学人教版七年级下册 第六章实数 单元卷（A）

一、选择题

二、填空题

三、解答题

2018-2019学年初中数学人教版七年级下册第六章实数单元卷（A）