2017年深圳市中考数学押题卷
试卷更新日期:2017-05-03 类型:中考模拟
一、选择题.
-
1. -2017的相反数是( ).A、2017 B、-2017 C、- D、2. 2017年“地球一小时”活动于3月19日举行,主题为“蓝生活”。据深圳供电局统计,今年深圳地球一小时时间全市用电量比上一小时减少电量17.97万度,将这个电量数用科学记数法表示为( ).
A、1.797× B、1.797× C、0.1797× D、17.97×3. 下列计算正确的是( )A、a2•a3=a6 B、(-2ab)2=4a2b2 C、(a2)3=a5 D、3a3b2÷a2b2=3ab4.与题干中平面图形有相同对称性的平面图形是( ).
 A、
A、 B、
B、 C、
C、 D、
D、 5.
5.如图是某工厂要设计生产的正六棱柱形密封罐的立体图形,它的主视图是( )
 A、
A、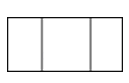 B、
B、 C、
C、 D、
D、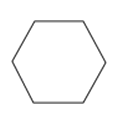 6. 某小组7位学生的中考体育成绩(满分30分)依次为27,30,29,27,30,28,30,则这组数据的众数与中位数分别是( ).A、30,27 B、30,29 C、29,30 D、30,287. 不等式组 的解集在数轴上表示为( ).
6. 某小组7位学生的中考体育成绩(满分30分)依次为27,30,29,27,30,28,30,则这组数据的众数与中位数分别是( ).A、30,27 B、30,29 C、29,30 D、30,287. 不等式组 的解集在数轴上表示为( ).
A、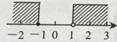 B、
B、 C、
C、 D、
D、 8.
8.二次函数y=ax²+bx+c的图像如图所示,则代数式(a+b)²-c²的值( ).
 A、大于0 B、等于0 C、小于0 D、不确定9. 如图,在 ABC中,AB=10,AC=8,BC=12,AD⊥BC于D,点E、F分别在AB、AC边上,把 ABC沿EF折叠,使点A与点D恰好重合,则 DEF的周长是( ).
A、大于0 B、等于0 C、小于0 D、不确定9. 如图,在 ABC中,AB=10,AC=8,BC=12,AD⊥BC于D,点E、F分别在AB、AC边上,把 ABC沿EF折叠,使点A与点D恰好重合,则 DEF的周长是( ). A、14 B、15 C、16 D、1710. 某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%。设把x公顷旱地改为林地,则可列方程( ).A、54-x=20%×108 B、54-x=20%(108+x) C、54+x=20%×162 D、108-x=20%(54+x)11. 如图,在 ABC中,AD平分 BAC,按如下步骤作图:
A、14 B、15 C、16 D、1710. 某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%。设把x公顷旱地改为林地,则可列方程( ).A、54-x=20%×108 B、54-x=20%(108+x) C、54+x=20%×162 D、108-x=20%(54+x)11. 如图,在 ABC中,AD平分 BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于 AD的长为半径在AD两侧做弧,交于两点M、N;
第二步,连接MN分别交AB、AC于点E、F;
第三步,连接DE、DF.
若BD=6,AF=4,CD=3,则BE的长是( ).
 A、2 B、4 C、6 D、812. 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将 ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将 CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
A、2 B、4 C、6 D、812. 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将 ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将 CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
① CMP∽ BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ;
⑤当 ABP≌ AND时,BP=4 -4.
A、①②③ B、②③⑤ C、①④⑤ D、①②⑤二、填空题.
-
13. 分解因式 =.14. 如图,四边形ABCD是菱形,E、F、G、H分别是各边的中点,随机地向菱形ABCD内部掷一粒米,则米粒落到阴影区域内的概率是.
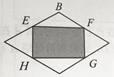 15.
15.在计算机程序中,二叉树是一种表示数据结构的方法。如图,一层二叉树的结点总数
为1,二层二叉树的结点总数为3,三层二叉树的结点总数为7…照此规律,七层二叉树的结点总数为.
 16. 如图,反比例函数y= (x>0)的图像交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=.
16. 如图,反比例函数y= (x>0)的图像交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=.
三、解答题.
-
17. 计算:| -2|+2cos45°- + .18. 先化简: ÷( - ),再从-2<x<3的范围内选取一个你喜欢的x值代入求值.
19. 某中学初二年级抽取部分学生进行跳绳测试,并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟100~109次的为中等;每分钟110~119次的为良好;每分钟120次及以上的为优秀。测试结果整理绘制成如下两幅不完整的统计图。请根据图中信息,解答下列各题: (1)、参加这次跳绳测试的共有人;(2)、补全条形统计图;(3)、在扇形统计图中,“中等”部分所对的圆心角的度数是;(4)、如果该校初二年级的总人数是480人,根据此统计数据,请你估算出该校初二年级跳绳成绩为“优秀”的人数。20. 如图,山坡上有一颗树AB,树底部B点到山脚C点的距离BC为6 米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.
(1)、参加这次跳绳测试的共有人;(2)、补全条形统计图;(3)、在扇形统计图中,“中等”部分所对的圆心角的度数是;(4)、如果该校初二年级的总人数是480人,根据此统计数据,请你估算出该校初二年级跳绳成绩为“优秀”的人数。20. 如图,山坡上有一颗树AB,树底部B点到山脚C点的距离BC为6 米,山坡的坡角为30°,小宇在山脚的平地F处测量这棵树的高,点C到测角仪EF的水平距离CF=1米,从E处测得树顶部A的仰角为45°,树底部B的仰角为20°,求树AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
 21. 我省某工艺厂为全运会设计了一款成本为每件20元的工艺品,投放市场试销后发现每天的销售量y(件)是售价x(元/件)的一次函数。当售价为22元/件时,每天销售量为780件;当售价为25元/件时,每天销售量为750件。
21. 我省某工艺厂为全运会设计了一款成本为每件20元的工艺品,投放市场试销后发现每天的销售量y(件)是售价x(元/件)的一次函数。当售价为22元/件时,每天销售量为780件;当售价为25元/件时,每天销售量为750件。
(1)、求y与x的函数关系式;
(2)、如果该工艺品售价最高不超过每件30元,那么售价定为每件多少元时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少元?(利润=售价-成本)
22. 如图,AB、CD为 O的直径,弦AE//CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使 PED= C. (1)、求证:PE是 O的切线;
(1)、求证:PE是 O的切线;
(2)、求证:ED平分 BEP;
(3)、若 O的半径为5,CF=2EF,求PD的长.
23. 如图,抛物线y=ax²-2ax-3a(a<0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC交于点M,且PM= AB. (1)、求抛物线的解析式;(2)、点K是x轴正半轴上一点,点A、P关于点K的对称点分别为 、 ,连接 、 ,若 ,求点K的坐标;(3)、矩形ADEF的边AF在x轴负半轴上,边AD在第二象限,AD=2,DE=3.将矩形ADEF沿x轴正方向平移t(t>0)个单位,直线AD、EF分别交抛物线于G、H.问:是否存在实数t,使得以点D、F、G、H为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、点K是x轴正半轴上一点,点A、P关于点K的对称点分别为 、 ,连接 、 ,若 ,求点K的坐标;(3)、矩形ADEF的边AF在x轴负半轴上,边AD在第二象限,AD=2,DE=3.将矩形ADEF沿x轴正方向平移t(t>0)个单位,直线AD、EF分别交抛物线于G、H.问:是否存在实数t,使得以点D、F、G、H为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,说明理由.