2018-2019学年数学八年级下册期中模拟试卷(浙江专版)
试卷更新日期:2019-03-29 类型:期中考试
一、选择题
-
1. 下列计算中正确的是( )A、
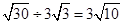 B、
B、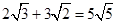 C、
C、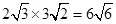 D、
D、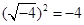 2. 若式子 有意义,则实数m的取值范围是( )A、m>﹣2 B、m>﹣2且m≠1 C、m≥﹣2 D、m≥﹣2且m≠13. 若(m+2) +3x﹣1=0是关于x的一元二次方程,则m的值为( )A、﹣2 B、± C、±2 D、04. 方程2(2x+1)(x-3)=0的两根分别为( )A、 和3 B、
2. 若式子 有意义,则实数m的取值范围是( )A、m>﹣2 B、m>﹣2且m≠1 C、m≥﹣2 D、m≥﹣2且m≠13. 若(m+2) +3x﹣1=0是关于x的一元二次方程,则m的值为( )A、﹣2 B、± C、±2 D、04. 方程2(2x+1)(x-3)=0的两根分别为( )A、 和3 B、 和3
C、 和
D、
和3
C、 和
D、 和
5. 某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如下表所示:
和
5. 某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如下表所示:读书时间(小时)
7
8
9
10
11
学生人数
6
10
9
8
7
则该班学生一周读书时间的中位数和众数分别是( )
A、9,8 B、9,9 C、9.5,9 D、9.5,86. 某超市一月份的营业额为200万元,三月份的营业额为288万元,如果每月比上月增长的百分数相同,则平均每月的增长( )A、10% B、15% C、20% D、25%7. 若三角形的两边长分别是4和6,第三边的长是方程x2-5x+6=0的一个根,则这个三角形的周长是( )A、13 B、16 C、12或13 D、11或168. 已知 , 则 最小值是( )A、6 B、3 C、﹣3 D、09. ( ﹣2)2008( +2)2007的值等于( )A、2 B、﹣2 C、 D、10. 根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图.
根据图所提供的信息,若要推荐一位成绩较稳定的选手去参赛,应推荐( )
A、李飞或刘亮 B、李飞 C、刘亮 D、无法确定二、填空题
-
11. 观察下列运算过程:
……
请运用上面的运算方法计算:
= .
12. 一组数据1,3,2,7, ,2,3的平均数是3,则该组数据的众数为 .
13. 如图,某小区有一块长为36m,宽为24m的矩形空地,计划在其中间修建两块形状相同的矩形绿地,它们的面积之和为600m2 , 两块绿地之间及周边有宽度相等的人行通道,则人行通道的宽度为m. 14. 若最简二次根式 与 是同类二次根式,则a= .15. 若关于x的一元二次方程(1﹣k)x2+2kx﹣k+1=0有实数根,则实数k的取值范围是 .16. 观察下列各式: ┉┉ 请你将猜想到的规律用含自然数n(n≥1)的代数式表示出来是.
14. 若最简二次根式 与 是同类二次根式,则a= .15. 若关于x的一元二次方程(1﹣k)x2+2kx﹣k+1=0有实数根,则实数k的取值范围是 .16. 观察下列各式: ┉┉ 请你将猜想到的规律用含自然数n(n≥1)的代数式表示出来是.三、解答题
-
17.
(1)、若5+ 的小数部分为a,5﹣ 的小数部分为b,求a2﹣b2的值.(2)、若:x= ,y= ,求 的值.18. 用适当方法解下列方程:(1)、x2+3x=0;(2)、(x+1)(x+2)=2x+4;(3)、x2-4x+1=0(用公式法).19. 解方程 时,我们可以将 看成一个整体,设 = ,则原方程可化为 ,解得 .当 =1时, =1,解得x=0,当 =2时, =2,解得x=1,所以原方程的解为 .请利用这种方法解方程: .
20. 阅读下列材料:求函数 的最大值.解:将原函数转化成关于 x 的一元二次方程,得 .
当 时,∵x为实数,∴△=
∴ 且 ;
当 时,
 即为 ,方程有解( 的值存在);
即为 ,方程有解( 的值存在);∴ .因此,
 的最大值为4.
的最大值为4.根据材料给你的启示,求函数 的最小值.
21. 已知a,b,c是△ABC的三边,试说明:(a2+b2﹣c2)2﹣4a2b2的值一定是负数.22. 甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):次数
运动员
1
2
3
4
5
甲
10
8
9
10
8
乙
10
9
9
a
b
某同学计算出了甲的成绩平均数是9,方差是
S甲2= [(10﹣9)2+(8﹣9)2+(9﹣9)2+(10﹣9)2+(8﹣9)2]=0.8,请作答:
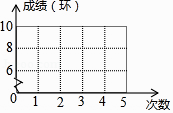 (1)、在图中用折线统计图将甲运动员的成绩表示出来;(2)、若甲、乙射击成绩平均数都一样,则a+b=;(3)、在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a、b的所有可能取值,并说明理由.23. 如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到点B为止,点Q以2cm/s的速度向点D移动.问:
(1)、在图中用折线统计图将甲运动员的成绩表示出来;(2)、若甲、乙射击成绩平均数都一样,则a+b=;(3)、在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a、b的所有可能取值,并说明理由.23. 如图,已知A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到点B为止,点Q以2cm/s的速度向点D移动.问: (1)、P、Q两点从开始出发多长时间时,四边形PBCQ的面积是33cm2?(2)、P、Q两点从开始出发多长时间时,点P与点Q之间的距离是10cm?
(1)、P、Q两点从开始出发多长时间时,四边形PBCQ的面积是33cm2?(2)、P、Q两点从开始出发多长时间时,点P与点Q之间的距离是10cm?