2018-2019学年初中数学人教版八年级下册期中模拟考试试卷
试卷更新日期:2019-03-28 类型:期中考试
一、选择题
-
1. 下列各式属于最简二次根式的是( )
A、 B、 C、 D、2. 若代数式 有意义,则 的取值范围是( )A、 且
且 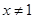 B、
B、 C、
C、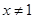 D、
D、 且
且 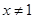 3. 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )
3. 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,则∠BCE的度数是( )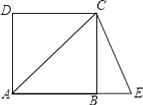 A、22.5° B、25° C、23° D、20°4.
A、22.5° B、25° C、23° D、20°4.如图,在矩形ABCD中,对角线AC、BD相交于点O,若∠ACB=30°,AB=2,则BD的长为( )
 A、4 B、3 C、2 D、15. 下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )A、1:2:3:4 B、2:2:3:3 C、2:3:2:3 D、2:3:3:2.6. 在平行四边形ABCD中,∠A:∠B:∠C:∠D的可能情况是( )A、2:7:2:7 B、2:2:7:7 C、2:7:7:2 D、2:3:4:57. 如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )
A、4 B、3 C、2 D、15. 下面给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( )A、1:2:3:4 B、2:2:3:3 C、2:3:2:3 D、2:3:3:2.6. 在平行四边形ABCD中,∠A:∠B:∠C:∠D的可能情况是( )A、2:7:2:7 B、2:2:7:7 C、2:7:7:2 D、2:3:4:57. 如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果EF=3,那么菱形ABCD的周长为( )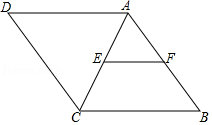 A、24 B、18 C、12 D、98. 已知a是1997的算术平方根的整数部分,b是1991的算术平方根的小数部分,则化简 的结果为( )A、 B、 C、 D、9. 将一组数 ,2, , , ,…, 按下面的方式进行排列: ,2, , , ; , , , ;…若 的位置记为(1,4), 的位置记为(2,2),则这组数中最大的有理数的位置记为( )A、(7,2) B、(7,5) C、(6,2) D、(6,3)10. 如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
A、24 B、18 C、12 D、98. 已知a是1997的算术平方根的整数部分,b是1991的算术平方根的小数部分,则化简 的结果为( )A、 B、 C、 D、9. 将一组数 ,2, , , ,…, 按下面的方式进行排列: ,2, , , ; , , , ;…若 的位置记为(1,4), 的位置记为(2,2),则这组数中最大的有理数的位置记为( )A、(7,2) B、(7,5) C、(6,2) D、(6,3)10. 如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )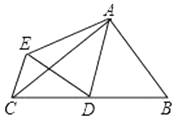 A、2 B、 C、 D、11. 下列命题中,是假命题的是( )A、在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形 B、在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形 C、在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形 D、在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形12. 如图,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODA交OA于点E,若AB=4,则线段OE的长为( )
A、2 B、 C、 D、11. 下列命题中,是假命题的是( )A、在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形 B、在△ABC中,若a2=(b+c) (b-c),则△ABC是直角三角形 C、在△ABC中,若∠B=∠C=∠A,则△ABC是直角三角形 D、在△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形12. 如图,正方形ABCD的对角线AC,BD相交于点O,DE平分∠ODA交OA于点E,若AB=4,则线段OE的长为( ) A、 B、4﹣2 C、 D、 ﹣2
A、 B、4﹣2 C、 D、 ﹣2二、填空题
-
13.
如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成对称图形戊,如图2所示,则图形戊的两条对角线长度之和是
 14. 已知矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4,则矩形对角线的长是 .15.
14. 已知矩形ABCD的对角线AC,BD相交于点O,∠AOB=60°,AB=4,则矩形对角线的长是 .15.学校有一块长方形的花圃如右图所示,有少数的同学为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了步(假设1米=2步),却踩伤了花草,所谓“花草无辜,踩之何忍”!
 16. 已知菱形的一条对角线长为6cm,面积为24cm2 , 则菱形的周长是 cm.17. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成了一个四边形ABCD,当线段AD=3时,线段BC的长为 .
16. 已知菱形的一条对角线长为6cm,面积为24cm2 , 则菱形的周长是 cm.17. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成了一个四边形ABCD,当线段AD=3时,线段BC的长为 .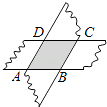 18. 观察下列各式:①;②=3;③ , …请用含n(n≥1)的式子写出你猜想的规律:
18. 观察下列各式:①;②=3;③ , …请用含n(n≥1)的式子写出你猜想的规律:三、解答题
-
19. 计算题:(1)、(2)、 .20.
已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC的中点.求证:四边形DFGE是平行四边形.
 21. 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3 米.求点B到地面的垂直距离BC.
21. 如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3 米.求点B到地面的垂直距离BC.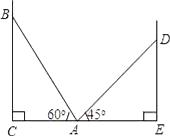 22.
22.如图,在▱ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
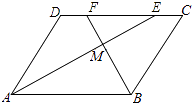 (1)、试说明:AE⊥BF;(2)、判断线段DF与CE的大小关系,并予以说明.23. 如图,等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.
(1)、试说明:AE⊥BF;(2)、判断线段DF与CE的大小关系,并予以说明.23. 如图,等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.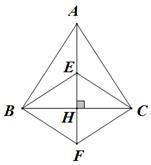 (1)、求证:四边形EBFC是菱形;(2)、如果∠BAC=∠ECF,求证:AC⊥CF.24. 已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)、求证:四边形EBFC是菱形;(2)、如果∠BAC=∠ECF,求证:AC⊥CF.24. 已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.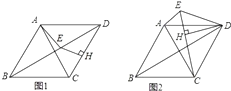 (1)、如图1,线段EH、CH、AE之间的数量关系是;(2)、如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.25.
(1)、如图1,线段EH、CH、AE之间的数量关系是;(2)、如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.25.在矩形ABCD中,∠DAB的平分线交BC于点E,交DC的延长线于点F,连接BD.
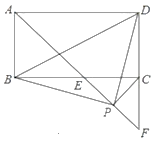 (1)、计算∠AEC的度数;(2)、求证:BE=DC;(3)、点P是线段EF上一动点(不与点E,F重合),在点P运动过程中,能否使△BDP成为等腰直角三角形?若能,写出点P满足的条件并证明;若不能,请说明理由.
(1)、计算∠AEC的度数;(2)、求证:BE=DC;(3)、点P是线段EF上一动点(不与点E,F重合),在点P运动过程中,能否使△BDP成为等腰直角三角形?若能,写出点P满足的条件并证明;若不能,请说明理由.