2018-2019学年初中数学人教版七年级下册期中模拟考试试卷

试卷更新日期：2019-03-28 类型：期中考试

进入出卷网下载

一、选择题

1. 下列运算：①a²•a³=a⁶ ， ②（a³）²=a⁶ ， ③a⁵÷a⁵=a，④（ab）³=a³b³ ，其中结果正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
2.
如图，已知∠1=70°，如果CD∥BE，那么∠B的度数为（）

A、70° B、100° C、110° D、120°

查看试题解析
3. 若a²=4，b²=9，且ab＜0，则a-b的值为（　　）

A、-2 B、±5 C、5 D、-5

查看试题解析
4. 下列说法正确的是（）

A、有理数都是有限小数 B、无限循环小数都是无理数 C、有理数和无理数都可以用数轴上的点表示 D、无理数包括正无理数，0和负无理数

查看试题解析
5. 如图，AB∥CD，∠1=45°，∠3=80°，则∠2的度数为（）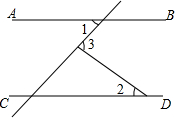

A、30° B、35° C、40° D、45°

查看试题解析
6.
如图，直线AB和CD相交于O，OE⊥AB，那么图中∠DOE与∠COA的关系是（　　）

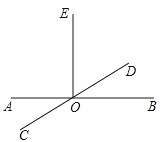A、对顶角 B、相等 C、互余 D、互补

查看试题解析
7. 由方程组 ${\begin{cases} x + m = 6 \\ y - 3 = m \end{cases}$ 可得出x与y的关系式是（）

A、 $x + y = 9$ B、 $x + y = 3$ C、 $x + y = - 3$ D、 $x + y = - 9$

查看试题解析
8. 下列各点中，位于第四象限的点是（）

A、(3，4) B、(－3，4) C、(3，－4) D、(－3，－4)

查看试题解析
9. 如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（﹣2，3），B（﹣3，1），C（﹣1，2），若将△ABC平移后，点A的对应点A₁的坐标为（1，2），则点C的对应点C₁的坐标为（）

A、（﹣1，5） B、（2，2） C、（3，1） D、（2，1）

查看试题解析
10. 如图，用直尺和三角尺画图：已知点P和直线a，经过点P作直线b，使b∥a，其画法的依据是（）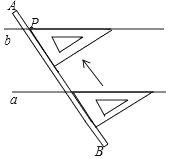

A、同位角相等，两直线平行 B、两直线平行，同位角相等 C、过直线外一点有且只有一条直线与已知直线平行 D、内错角相等，两直线平行

查看试题解析
11. 下列语句正确的是（　　）

A、一个数的立方根不是正数就是负数 B、负数没有立方根 C、如果一个数的立方根是这个数本身，那么这个数一定是零 D、一个数的立方根与这个数同号，零的立方根是零

查看试题解析
12. 如图，AB∥CD，EF交AB、CD于点E、F、EG平分∠BEF，交CD于点G．若∠1=40°，则∠EGF=（）

A、20° B、40° C、70° D、110°

查看试题解析

二、填空题

13. 下列各数： $3 \sqrt{2}$ ， $- \frac{5}{14}$ ， $\sqrt[3]{- 27}$ ，1.414， $- \frac{π}{3}$ ，3.12122， $- \sqrt{9}$ ，3.161661666…（每两个1之间依次多1个6）中，无理数有个，有理数有个，负数有个，整数有个．

查看试题解析
14. ﹣ $\frac{1}{\sqrt{3}}$ 的绝对值的倒数是．

查看试题解析
15. 如图所示，将含有30°角的三角板的直角顶点放在互相平行的两条直线其中一条上，若∠1=35°，则∠2的度数为度

查看试题解析
16. 一个正数的平方根分别是x+1和x﹣5，则x= ．

查看试题解析
17. 点P（3，5）到x轴的距离有个单位长度，到y轴的距离有个单位长度．

查看试题解析
18. 如图，△ABC中，点D在BA的延长线上，DE∥BC，如果∠BAC=80°，∠C=33°，那么∠BDE的度数是.

查看试题解析

三、计算题

19. 解方程：（1）4x²-9=0 (2)x(x-2)+x-2=0

查看试题解析
20. 计算：

(1)、 ${(\sqrt{3})}^{2} - \sqrt[3]{-64} - \sqrt{3^{2} + 4^{2}}$ ;

(2)、 $| -3 | + {(π + 1)}^{0} - \sqrt{9} + \sqrt[3]{8}$

查看试题解析

四、解答题

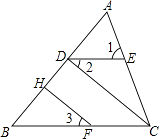
21. 已知x是16的算术平方根，y是9的平方根，求x²+y²+x﹣2的值．

查看试题解析
22. 如图，∠1=∠ACB，∠2=∠3，FH⊥AB于H．问CD与AB有什么关系？并说明理由．

查看试题解析
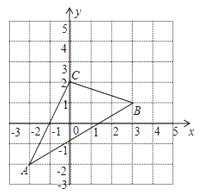
23.
如图，△ABC在直角坐标系中，
（1）请写出△ABC各点的坐标．
（2）若把△ABC向上平移2个单位，再向左平移1个单位得到△A′B′C′，写出 A′、B′、C′的坐标，并在图中画出平移后图形．
（3）求出三角形ABC的面积．

查看试题解析
24.
如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补．

(1)、试判断直线AB与直线CD的位置关系，并说明理由；

(2)、如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；

(3)、如图3，在（2）的条件下，连接PH，K是GH上一点使∠PHK=∠HPK，作PQ平分∠EPK，问∠HPQ的大小是否发生变化？若不变，请求出其值；若变化，说明理由．

查看试题解析
25. 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起（其中，∠A=60°，∠D=30°，∠E=∠B=45°）

(1)、① 若∠DCE=35°，则∠ACB=°②若∠ACB=140°，则∠DCE=°

(2)、由（1）猜想，∠ ACB与∠DCE 的数量关系：

(3)、当∠ACE<180°，且点E在直线AC上方时，这两块三角尺是否存在一组边互相平行？若存在，请直接写出∠ACE角度所有可能的值（不必说明理由），若不存在，说明理由。

查看试题解析
26. 长江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况．如图，灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是a°/秒，灯B转动的速度是b°/秒，且a、b满足|a﹣3b|+（a+b﹣4）²=0．假定这一带长江两岸河堤是平行的，即PQ∥MN，且∠BAN=45°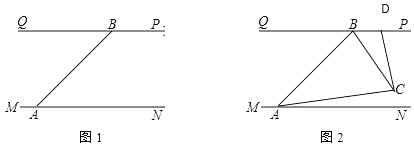

(1)、求a、b的值；

(2)、若灯B射线先转动20秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？

(3)、如图，两灯同时转动，在灯A射线到达AN之前．若射出的光束交于点C，过C作CD⊥AC交PQ于点D，则在转动过程中，∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请求出其取值范围．

查看试题解析