2017年山东省日照市莒县南四校联盟中考数学一模试卷

试卷更新日期：2017-05-02 类型：中考模拟

进入出卷网下载

一、选择题

1. $- \frac{1}{3}$ 的倒数是（）

A、﹣3 B、 $- \frac{1}{3}$ C、3 D、 $\frac{1}{3}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{3}$ + $\sqrt{2}$ = $\sqrt{6}$ B、x⁶÷x³=x² C、 $\sqrt{4}$ =2 D、a²（﹣a²）=a⁴

查看试题解析
3. PM2.5是指大气中直径≤0.0000025米的颗粒物，将0.0000025用科学记数法表示为（）

A、2.5×10^﹣⁷ B、2.5×10^﹣⁶ C、25×10^﹣⁷ D、0.25×10^﹣⁵

查看试题解析
4. 在函数y= $\sqrt{1 - 2 x}$ 中，自变量x的取值范围是（）

A、x＜ $\frac{1}{2}$ B、x≤ $\frac{1}{2}$ C、x＞ $\frac{1}{2}$ D、x≥ $\frac{1}{2}$

查看试题解析
5. 不等式5x﹣1＞2x+5的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 一个袋子中装有3个红球和2个黄球，这些球的形状、大小．质地完全相同，在看不到球的条件下，随机从袋子里同时摸出2个球，其中2个球的颜色相同的概率是（）

A、 $\frac{3}{4}$ B、 $\frac{1}{5}$ C、 $\frac{3}{5}$ D、 $\frac{2}{5}$

查看试题解析
7. 如图是由几个小立方块所搭几何体的俯视图，小正方形的数字表示在该位置的小立方块的个数，这个几何体的主视图是（）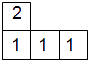

A、 B、 C、 D、

查看试题解析
8. 小玲每天骑自行车或步行上学，她上学的路程为2800米，骑自行车的平均速度是步行平均速度的4倍，骑自行车比步行上学早到30分钟．设小玲步行的平均速度为x米/分，根据题意，下面列出的方程正确的是（）

A、 $\frac{2800}{x} - \frac{2800}{4 x} = 30$ B、 $\frac{2800}{4 x} - \frac{2800}{x} = 30$ C、 $\frac{2800}{x} - \frac{2800}{5 x} = 30$ D、 $\frac{2800}{5 x} - \frac{2800}{x} = 30$

查看试题解析
9. 关于x的一元二次方程kx²+3x﹣1=0有实数根，则k的取值范围是（）

A、k≤﹣ $\frac{9}{4}$ B、k≤﹣ $\frac{9}{4}$ 且k≠0 C、k≥﹣ $\frac{9}{4}$ D、k≥﹣ $\frac{9}{4}$ 且k≠0

查看试题解析
10. 下列命题中，原命题与逆命题均为真命题的有（）
①若|a|=|b|，则a²=b²；②若ma²＞na² ，则m＞n；
③垂直于弦的直径平分弦；④对角线互相垂直的四边形是菱形．

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 如图，⊙O过点B、C，圆心O在等腰直角三角形ABC的内部，∠BAC=90°，OA=1，BC=6，则⊙O的半径为（）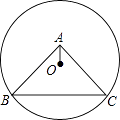

A、6 B、13 C、 $\sqrt{13}$ D、2 $\sqrt{13}$

查看试题解析
12. 函数y=x²+bx+c与y=x的图象如图所示，有以下结论：
①b²﹣4c＞0；
②b+c+1=0；
③3b+c+6=0；
④当1＜x＜3时，x²+（b﹣1）x+c＜0．
其中正确的个数为（）

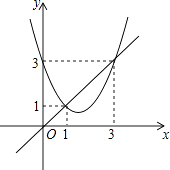A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y= $\frac{k}{x}$ 的图象上，若点A的坐标为（4，﹣2），则k的值为．

查看试题解析
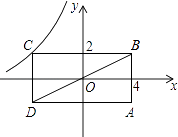14.
如图，在▱ABCD中，E在AB上，CE、BD交于F，若AE：BE=4：3，且BF=2，则BD= ．

查看试题解析
15. 如图，已知点A、B、C、D均在以BC为直径的圆上，AD∥BC，AC平分∠BCD，∠ADC=120°，四边形ABCD的周长为10，则图中阴影部分的面积为．

查看试题解析
16. 如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE= $\frac{1}{3}$ AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（填序号）

查看试题解析

三、解答题

17.
某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动，现从中随机抽取部分作品，按A，B，C，D四个等级进行评价，并根据结果绘制了如下两幅不完整的统计图．

(1)、求抽取了多少份作品；

(2)、此次抽取的作品中等级为B的作品有，并补全条形统计图；

(3)、若该校共征集到800份作品，请估计等级为A的作品约有多少份．

查看试题解析
18. 如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．已知原传送带AB长为4米．

(1)、求新传送带AC的长度；

(2)、如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点4米的货物MNQP是否需要挪走，并说明理由．（说明：（1）（2）的计算结果精确到0.1米，参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73， $\sqrt{3}$ ≈2.24， $\sqrt{6}$ ≈2.45）

查看试题解析
19. 我国中东部地区雾霾天气趋于严重，环境治理已刻不容缓．我市某电器商场根据民众健康需要，代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务．

(1)、试确定月销售量y（台）与售价x（元/台）之间的函数关系式；并求出自变量x的取值范围；

(2)、当售价x（元/台）定为多少时，商场每月销售这种空气净化器所获得的利润w（元）最大？最大利润是多少？

查看试题解析
20. 已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．

(1)、求证：点D是AB的中点；

(2)、判断DE与⊙O的位置关系，并证明你的结论；

(3)、若⊙O的直径为18，cosB= $\frac{1}{3}$ ，求DE的长．

查看试题解析
21.
如图，在正方形ABCD中，对角线AC与BD相交于点O，点E是BC上的一个动点，连接DE，交AC于点F．

(1)、如图①，当 $\frac{C E}{E B} = \frac{1}{3}$ 时，求 $\frac{S_{△ C E F}}{S_{△ C D F}}$ 的值；

(2)、如图②当DE平分∠CDB时，求证：AF= $\sqrt{2}$ OA；

(3)、如图③，当点E是BC的中点时，过点F作FG⊥BC于点G，求证：CG= $\frac{1}{2}$ BG．

查看试题解析
22.
已知：在平面直角坐标系中，抛物线 $y = - \frac{1}{4} x^{2} + b x + 3$ 交x轴于A、B两点，交y轴于点C，且对称轴为x=﹣2，点P（0，t）是y轴上的一个动点．

(1)、求抛物线的解析式及顶点D的坐标．

(2)、如图1，当0≤t≤4时，设△PAD的面积为S，求出S与t之间的函数关系式；S是否有最小值？如果有，求出S的最小值和此时t的值．

(3)、如图2，当点P运动到使∠PDA=90°时，Rt△ADP与Rt△AOC是否相似？若相似，求出点P的坐标；若不相似，说明理由．

查看试题解析