2017年山东省莒北五校联盟中考数学一模试卷
试卷更新日期：2017-05-02 类型：中考模拟
一、选择题
-
1. ﹣2017的绝对值是（ ）A、2017 B、 C、﹣2017 D、﹣2. 下列各图是选自历届世博会徽中的图案，其中是中心对称图形的是（ ）A、
B、
C、
D、
3. 下列事件中是必然事件的是（ ）A、﹣a是负数 B、两个相似图形是位似图形 C、随机抛掷一枚质地均匀的硬币，落地后正面朝上 D、平移后的图形与原来对应线段相等4. 据统计，某年我国国内生产总值达397983亿元．则以亿元为单位用科学记数法表示这一年我国的国内生产总值为（ ）亿元．A、3.97983×1013 B、3.97983×105 C、4.0×1013 D、4.0×1055. 如图所示，AB∥CD，AD与BC相交于点E，EF是∠BED的平分线，若∠1=30°，∠2=40°，则∠BEF=（ ）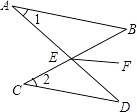
A、70° B、40° C、35° D、30°6. 如图是由5个底面直径与高度相等的大小相同的圆柱搭成的几何体，其左视图是（ ）
A、
B、
C、
D、
7. 若关于x的方程x2+3x+a=0有一个根为1，则另一个根为（ ）A、﹣4 B、2 C、4 D、﹣38. 如图，在边长为12的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G．则BG的长为（ ）
A、5 B、4 C、3 D、29. 若不等式组 有解，则实数a的取值范围是（ ）A、a≥﹣2 B、a＜﹣2 C、a≤﹣2 D、a＞﹣210.如图①，在平面直角坐标系中，平行四边形ABCD在第一象限，且AB∥x轴，直线y=﹣x从原点出发沿x轴正方向平移，被平行四边形ABCD截得的线段EF的长度l与平移的距离m的函数图象如图②，那么平行四边形ABCD的面积为（ ）
A、4 B、 C、8 D、11. 如图，AB为半圆O的直径，CD切⊙O于点E，AD、BC分别切⊙O于A、B两点，AD与CD相交于D，BC与CD相交于C，连接OD、OC，对于下列结论：①OD2=DE•CD；②AD+BC=CD；③OD=OC；④S梯形ABCD=CD•OA；⑤∠DOC=90°；⑥若切点E在半圆上运动（A、B两点除外），则线段AD与BC的积为定值．其中正确的个数是（ ）
A、5 B、4 C、3 D、2二、填空题
-
12. 分解因式：a3﹣2a2+a= ．13. 如图，四边形ABCD是菱形，∠A=60°，AB=6，扇形BEF的半径为6，圆心角为60°，则图中阴影部分的面积是 ．
14. 关于x的分式方程 的解为正数，则m的取值范围是 ．15. 两个反比例函数y= （k＞1）和y= 在第一象限内的图象如图所示，点P在y= 的图象上，PC⊥x轴于点C，交y= 的图象于点A，PD⊥y轴于点D，交y= 的图象于点B，BE⊥x轴于点E，当点P在y= 图象上运动时，以下结论：①BA与DC始终平行；②PA与PB始终相等；③四边形PAOB的面积不会发生变化；④△OBA的面积等于四边形ACEB的面积．其中一定正确的是（填序号）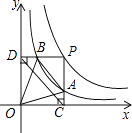
三、解答题
-
16. 计算： ﹣3tan30°+（π﹣4）0 ．17.
一个长方体木箱沿斜面下滑，当木箱滑至如图位置时，AB=3m，已知木箱高BE= ，斜面坡角为30°，求木箱端点E距地面AC的高度EF．
18. 某电脑公司经销甲种型号电脑，今年三月份的电脑售价比去年同期每台降价1000元，如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元．(1)、今年三月份甲种电脑每台售价多少元？(2)、为了增加收入，电脑公司决定再经销乙种型号电脑．已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台，有几种进货方案？19.2015年1月，市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价．评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查，了解他们每天在课外用于学习的时间，并绘制成如下不完整的统计图．
根据上述信息，解答下列问题：
(1)、本次抽取的学生人数是；扇形统计图中的圆心角α等于；补全统计直方图；(2)、被抽取的学生还要进行一次50米跑测试，每5人一组进行．在随机分组时，小红、小花两名女生被分到同一个小组，请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率．20. 某商品的进价为每件40元，如果售价为每件50元，每个月可卖出210件；如果售价超过50元但不超过80元，每件商品的售价每上涨1元，则每个月少卖1件；如果售价超过80元后，若再涨价，则每涨1元每月少卖3件．设每件商品的售价为x元，每个月的销售量为y件．(1)、求y与x的函数关系式并直接写出自变量x的取值范围；(2)、设每月的销售利润为W，请直接写出W与x的函数关系式；(3)、每件商品的售价定位多少元时，每个月可获得最大利润？最大的月利润是多少元？
