数学(苏科版)八年级下册第11章 11.2反比例函数的图像与性质 同步练习
试卷更新日期:2017-05-02 类型:同步测试
一、单选题
-
1. 函数y=mx+n与y= ,其中m≠0,n≠0,那么它们在同一坐标系中的图像可能是( )A、
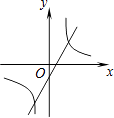 B、
B、 C、
C、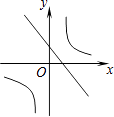 D、
D、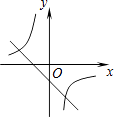 2. 如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ,则k的值是( )
2. 如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ,则k的值是( )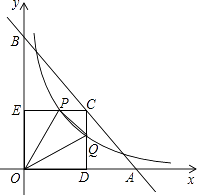 A、4 B、2 C、 D、3. 已知反比例函数y= 的图象经过点A(﹣1,2),那么,k=( )A、2 B、﹣2 C、 D、﹣4. 点A为反比例函数图象上一点,它到原点的距离为5,则x轴的距离为3,若点A第二象限内,则这个函数的解析式为( )A、y= B、y=﹣ C、y= D、y=﹣5. 如图,反比例函数 的图象经过点A,则当x=﹣1时,y的值是( )
A、4 B、2 C、 D、3. 已知反比例函数y= 的图象经过点A(﹣1,2),那么,k=( )A、2 B、﹣2 C、 D、﹣4. 点A为反比例函数图象上一点,它到原点的距离为5,则x轴的距离为3,若点A第二象限内,则这个函数的解析式为( )A、y= B、y=﹣ C、y= D、y=﹣5. 如图,反比例函数 的图象经过点A,则当x=﹣1时,y的值是( )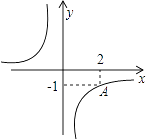 A、2 B、﹣2 C、 D、-6. 在反比例函数y= 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( ).
A、2 B、﹣2 C、 D、-6. 在反比例函数y= 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( ).
A、k>1 B、k>0 C、k≥1 D、k<17. 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )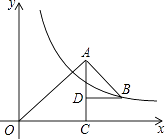 A、36 B、12 C、6 D、38. 若点(-2,y1)、(-1,y2)、(1,y3)在反比例函数 的图像上,则下列结论中正确的是( )
A、36 B、12 C、6 D、38. 若点(-2,y1)、(-1,y2)、(1,y3)在反比例函数 的图像上,则下列结论中正确的是( )
A、y1>y2>y3 B、y2>y1>y3 C、y3>y1>y2 D、y3>y2>y19. 如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点B,点C、D在x轴上,且BC∥AD,四边形ABCD的面积为3,则这个反比例函数的解析式为( )
A、 B、 C、 D、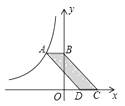
二、填空题
-
10. 已知点A在反比例函数y= 的图像上,点B与点A关于原地对称,BC∥y轴,与反比例函数y=﹣ 的图像交于点C,连接AC,则△ABC的面积为 .
 11. 如图,y1= x+1与双曲线y2= 的两个交点A,B的纵坐标分别为﹣1,2,则使得y2<y1<0成立的自变量x的取值范围是 .
11. 如图,y1= x+1与双曲线y2= 的两个交点A,B的纵坐标分别为﹣1,2,则使得y2<y1<0成立的自变量x的取值范围是 .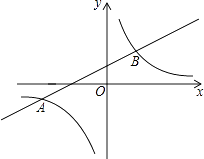 12. 已知反比例函数 (m是常数)的图像在一、三象限,则m的取值范围为 .13. 已知 与y=x﹣6相交于点P(a,b),则 的值为 .14. 如图,点P、Q是反比例函数y= 图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”)
12. 已知反比例函数 (m是常数)的图像在一、三象限,则m的取值范围为 .13. 已知 与y=x﹣6相交于点P(a,b),则 的值为 .14. 如图,点P、Q是反比例函数y= 图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”) 15. 如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥y轴,C,D在y轴上,若四边形ABCD为平行四边形,则它的面积为 .
15. 如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥y轴,C,D在y轴上,若四边形ABCD为平行四边形,则它的面积为 .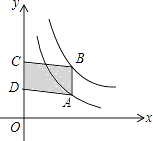 16. 已知变量y与x成反比,当x=1时,y=﹣6,则当y=3时,x= .17. 反比例函数的图象经过点(﹣1,2),则它的解析式是 , 图象位于象限.18. 如图,正比例函数y=x与反比例函数y= 的图像交于点A、点C,AB⊥x轴于点B,CD⊥x轴于点D,则四边形ABCD的面积为 .
16. 已知变量y与x成反比,当x=1时,y=﹣6,则当y=3时,x= .17. 反比例函数的图象经过点(﹣1,2),则它的解析式是 , 图象位于象限.18. 如图,正比例函数y=x与反比例函数y= 的图像交于点A、点C,AB⊥x轴于点B,CD⊥x轴于点D,则四边形ABCD的面积为 .
三、解答题
-
19. 如图是函数 与函数 在第一象限内的图象,点P是 的图象上一动点,PA⊥x轴于点A , 交 的图象于点C, PB⊥y轴于点B , 交 的图象于点D.
 (1)、求证:D是BP的中点;(2)、求出四边形ODPC的面积.
(1)、求证:D是BP的中点;(2)、求出四边形ODPC的面积.
20. 如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y= 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m , 0).其中m>0. (1)、四边形ABCD的是 . (填写四边形ABCD的形状)(2)、当点A的坐标为(n , 3)时,四边形ABCD是矩形,求mn的值.
(1)、四边形ABCD的是 . (填写四边形ABCD的形状)(2)、当点A的坐标为(n , 3)时,四边形ABCD是矩形,求mn的值.
(3)、试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
四、综合题
