数学（苏科版）八年级下册第9章 9.4矩形、菱形、正方形 同步练习
试卷更新日期：2017-05-02 类型：同步测试
一、单选题
-
1. 下面说法中，正确的是（ ）A、有一个角是直角的四边形是矩形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是矩形 D、四个角都是直角的四边形是矩形2. 在▱ABCD中增加下列条件中的一个，这个四边形就是矩形，则增加的条件是（ ）A、对角线互相平分 B、AB=BC C、∠A+∠C=180° D、AB= AC3. 检查一个门框是矩形的方法是（ ）A、测量两条对角线是否相等 B、测量有三个角是直角 C、测量两条对角线是否互相平分 D、测量两条对角线是否互相垂直4. 在下列所给出的4个图形中，对角线一定互相垂直的是（ ）A、
长方形
B、
平行四边形
C、
菱形
D、
直角梯形
5.如图，矩形ABCD对角线相交于点O ， ∠AOB＝60°，AB＝4，则AC的为 （ ）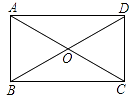
A、4 B、8 C、4 D、106.如图，菱形ABCD中，∠BAD＝120°．若△ABC的周长是15，则菱形ABCD的周长是（ ）
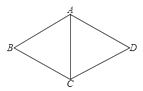A、25 B、20 C、15 D、107.如图，以正方形ABCD的一边向形外作等边△ABE，BD与EC交于点F，则∠AFD等于（ ）
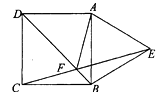A、60° B、50° C、45° D、40°8.如图，将矩形ABCD分成15个大小相等的正方形，E、F、G、H分别在AD、AB、BC、CD边上，且都是某个小正方形的顶点，若四边形EFGH的面积为1，则矩形ABCD的面积为（ ）
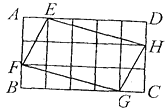A、2 B、3 C、 D、9. 如图，在矩形ABCD中，若AC=2AB，则∠AOB的大小是（ ）
A、30° B、45° C、60° D、90°10. 如图，四边形ABCD的四边相等，且面积为120cm2 ， 对角线AC=24cm，则四边形ABCD的周长为（ ）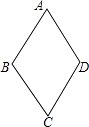
A、52cm B、40cm C、39cm D、26cm11. 在直线L上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4 ， 则S1+2S2+2S3+S4=（ ）
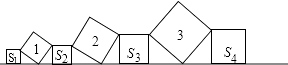A、5 B、4 C、6 D、1012. 八个边长为1的正方形如图摆放在平面直角坐标系中，经过P点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（ ）
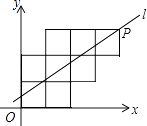A、 B、y= x+ C、 D、二、填空题
-
13. 如图，平行四边形ABCD的对角线AC，BD交于点O，△AOD是正三角形，AD=4，则平行四边形ABCD的面积为 ．
14. 如图，两条宽度为1的带子，相交成∠α，那么重叠部分（阴影部分）的面积是 ．
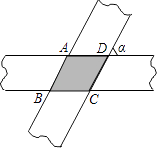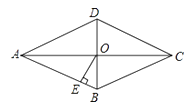
15. 如图，BF平行于正方形ABCD的对角线AC，点E在BF上，且AE=AC，CF∥AE，则∠BCF的度数为 ．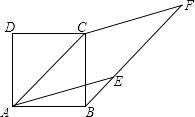
16. 在四边形ABCD中，∠A=∠B=∠C=∠D，则四边形ABCD是 ．17. 一组邻边相等的是正方形，有一个角是角的菱形是正方形．18.如图，在菱形ABCD中，对角线AC与BD相交于点O，OE⊥AB，垂足为E点，若∠ADC=130°，
则∠AOE= ．
三、解答题
-
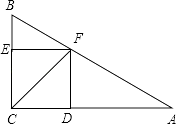
19. 如图，△ABC中，∠C=90°，∠BAC、∠ABC的平分线相交于点D，DE⊥BC，DF⊥AC，垂足分别为E、F．问四边形CFDE是正方形吗？请说明理由．
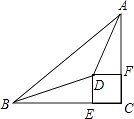20. 如图所示，在Rt△ABC中，CF为直角的平分线，FD⊥CA于D，FE⊥BC于E，则四边形CDFE是怎样的四边形，为什么？
